In the covid-19 era, social distancing has emerged as an important factor in the fight against the disease. We change our habits and the way we interact with others, so that we minimize the chances that the virus can be transmitted.
Social distancing includes rules about how close we can be to one another. When we are brought together, we must maintain a certain distance between ourselves.
Then a problem emerges: if we have a given space, how many people can fit into the space, while respecting social distancing rules? And where should they be placed?
We can represent each person as a circle whose radius is equal to the minimum distance we must maintain. Then the problem is to insert the circles with the given radius inside a shape that describes the space we want to fill.
To find where the circles should be placed, we can work as follows:
-
We put a circle at the point where we want to start the placement process.
-
We put a circle tangent to the first one, noting that each circle follows the other.
-
We interpolate a circle tangent to the last circle and the first circle we inserted, noting that it comes between them. We repeat this step to add more circles.
This is how the process will evolve for the first seven circles:
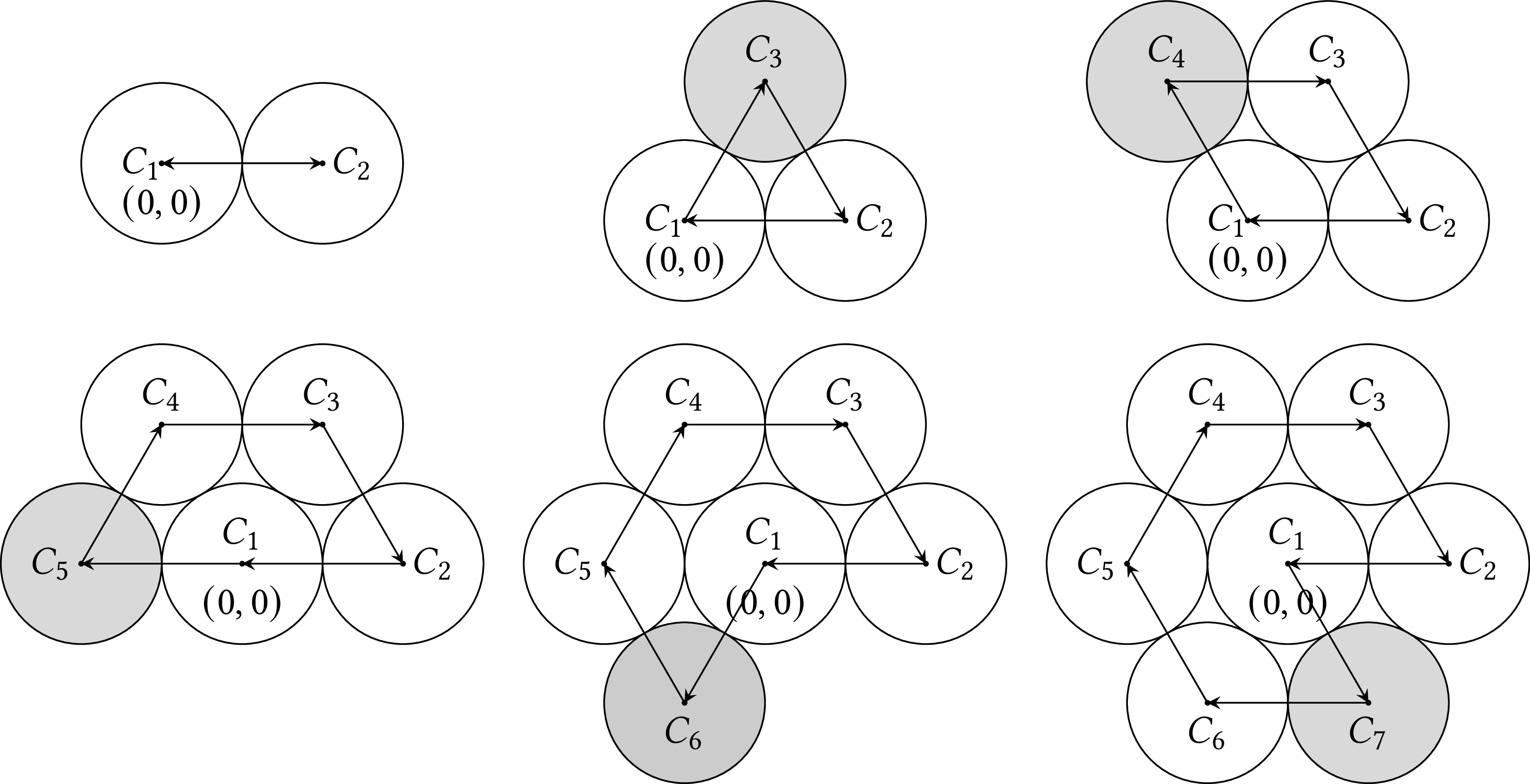
We can observe that the centers of the circles form a closed polygon. If we want to continue the process, we must remove from the polygon vertex $C_1$ and connect directly vertices $C_2$ and $C_7$. Then we can interpolate a circle tangent to $C_2$ and $C_7$, as in the first panel of the next figure.
This suggests an idea. Let us call the circles on the perimeter, next to whom we can attach tangential circles, the front. To add circles, we follow these steps:
-
We add the first two circles (these two form a trivial front).
-
We find the circle in the front that is closest to our starting point. Suppose that this circle $C_m$. If there are more than one circles with the same distance, we pick the one that was inserted earliest.
-
We try to interpolate a circle between $C_m$ and its successor in the front, $C_n$. Let us call this circle $C_i$.
-
If $C_i$ does not intersect with any of the front's cirles, we insert it into our shape and we return to step 2.
-
Otherwise, we remove from the front the problematic circles and we then return to step 2.
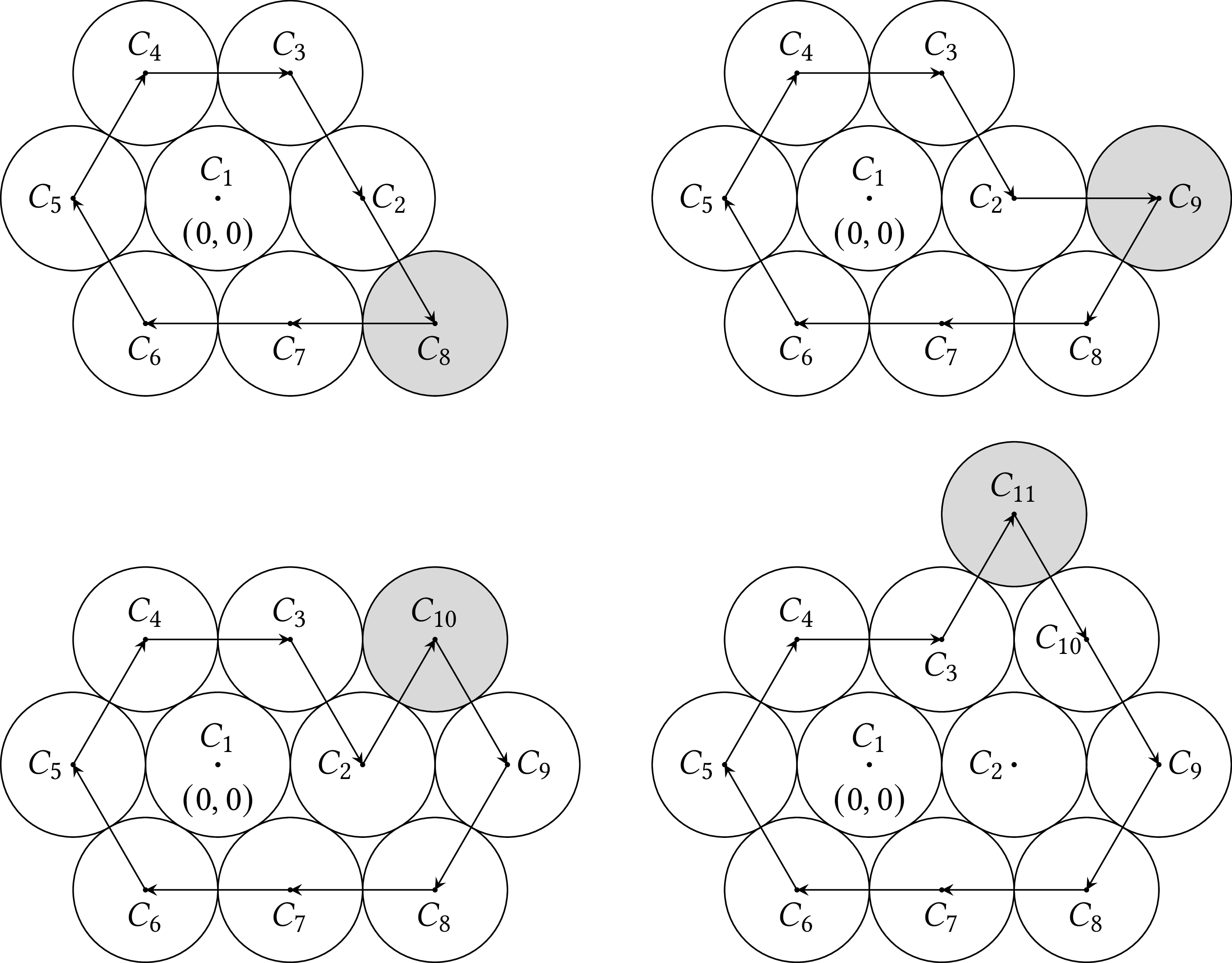
If we continue in this way we can insert circles $C_9$ and $C_{10}$ without a problem. Then, the circle in the front that was inserter earliest and is closest to our starting point is $C_2$, whose successor is $C_{10}$. If we try to interpolate a circle between $C_2$ and $C_{10}$, we will find out that it falls on $C_3$. According to step 5, we remove $C_2$ from the front, so now we have $C_3$ followed by $C_{10}$ in the front. Returning to step 2 we find that $C_3$ is the front circle closest to the starting point, so we add circle $C_{11}$.
That is not a complete algorithm, because step 5 is not clear. We have termed some circles "problematic", but we have not really defined which they are that they should be removed from the front.
If we return to our example, we saw that, as the circle we try to insert between $C_2$ and $C_{10}$ intersects $C_3$, we removed $C_2$ from the front. In general, if the circle $C_i$ that we are trying to insert tangential to $C_m$ and $C_n$ intersects a circle $C_j$ that comes before $C_m$ in the front, we remove from the front the circles from the successor of $C_j$ up to and including $C_m$ and $C_j$ becomes the new $C_m$, as you can see in the following figure—do not be surprised that the circles do not all have the same radius, we would like our algorithm to work even when the circles are not equal.

If the circles are not equal, there is another possibility, that of $C_i$ intersecting a circle $C_j$ that comes after $C_n$ in the front. Then we remove from the front the circles from $C_n$ up to and including the predecessor of $C_j$ and $C_j$ becomes the new $C_n$, as shown in the following figure.

Of course, as the centers of the circles that constitute the front are connected in a closed polygon, a circle that follows another circle also precedes it, if we continue going round. Moreover, the circle we are trying to insert can intersect with two circles in the front; see the next figure. Again, do not be surprised at the strange shape of the front, we will see that the solution we will find will work even in such cases, which can arise when the front grows while it fills a bounded shape.
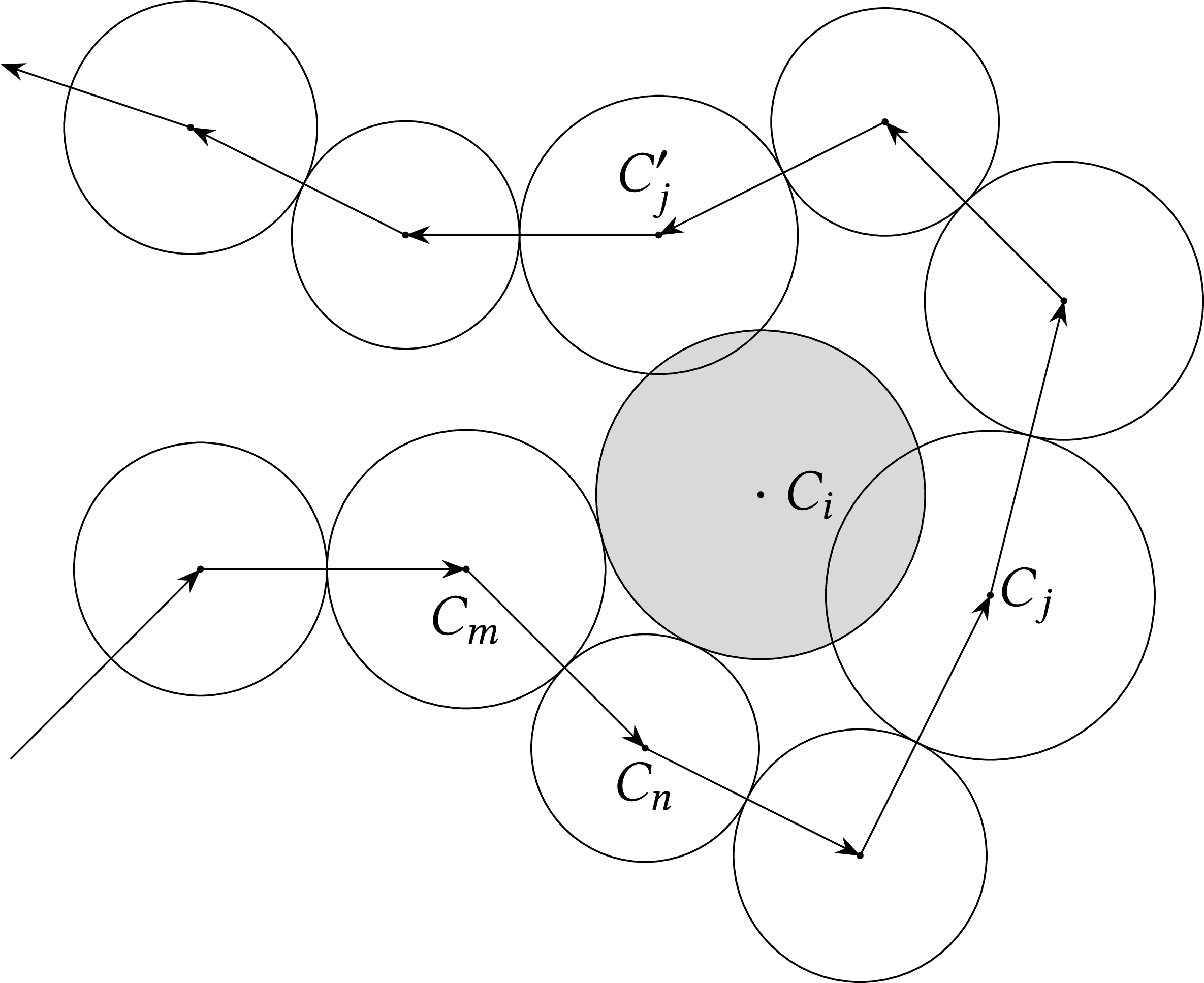
To detect the offending circle $C_j$ in all situations, we start from $C_n$ and we proceed in the front till we meet $C_m$. We take note of the first circle that is intersected by $C_i$, $C_j$, and the last, $C_{j}'$; if $C_i$ intersects only one circle, then $C_j = C_{j}'$. We count how many circles are between $C_n$ and $C_j$, say $b_{nj}$, and how many there are between $C_m$ and $C_{j}'$, say $b_{mj'}$. If $b_{mj'} < b_{nj}$, then we take as $C_j$ the circle $C_{j'}$ that comes before $C_m$. Otherwise, we take the circle $C_j$ that comes after $C_n$.
If for every circle in the front we keep not only its successor but also its predecessor, then we can find $C_j$ in another way. We start from $C_n$ and we walk one successor circle at a time towards $C_m$. At the same time, we start from $C_m$ and we walk one predecessor circle at a time towards $C_n$. That means that we go one step in each direction of the front. If we find an intersecting circle in either direction, or if we go beyond the middle of the front, we stop. If we stopped because we found an intersecting circle, we check whether we found it going along the successor or the predecessor circles.
Our algorithm then evolves to this:
-
We add the first two circles (these two form a trivial front).
-
We find the circle in the front that is closest to our starting point. Suppose that this circle $C_m$. If there are more than one circles with the same distance, we pick the one that was inserted earliest.
-
We try to interpolate a circle between $C_m$ and its successor in the front, $C_n$. Let us call this circle $C_i$.
-
If $C_i$ does not intersect with any of the front's cirles, we insert it into our shape and we return to step 2.
-
Otherwise:
-
If $C_i$ intersects a circle $C_j$ that precedes $C_m$, we take out from the front the circles from the successor of $C_j$ up to and including $C_m$, we let $C_j$ be the new $C_m$, and we return to step 3.
-
If $C_i$ intersects a circle $C_j$ that follows $C_n$, we take out from the front the circles from $C_n$ up to and including the predecessor of $C_j$, we let $C_j$ be the new $C_n$, and we return to step 3.
-
Our algorithm now works and will fill out the plane, beginning from the starting point. But it does not detect where it should stop because it has reached the boundary of the space we want to fill. To achieve that, we have to do some more work. We will now make a distinction between those circles of the front to which we can attach a tangent circle without breaching the boundaries that have been set. We will call these circles alive. When a circle is inserted into the front, it is alive. The algorithm then will further evolve to this:
-
We add the first two circles (these two form a trivial front).
-
We want to insert the $i$th circle. We find the circle in the front that is closest to our starting point. Suppose that this circle $C_m$. If there are more than one circles with the same distance, we pick the one that was inserted earliest.
-
We try to interpolate a circle between $C_m$ and its successor in the front, $C_n$. Let us call this circle $C_i$.
-
If $C_i$ intersects a circle of the front:
-
If $C_i$ intersects a circle $C_j$ that precedes $C_m$, we take out from the front and kill the circles from the successor of $C_j$ up to and including $C_m$, we let $C_j$ be the new $C_m$, and we return to step 3.
-
If $C_i$ intersects a circle $C_j$ that follows $C_n$, we take out from the front and kill the circles from $C_n$ up to and including the predecessor of $C_j$, we let $C_j$ be the new $C_n$, and we return to step 3.
-
-
At this point we have found a circle $C_i$ that does not intersect any circle in the front. We then check whether it breaches the boundaries of our shape.
-
If it does, then the circle $C_m$ that we picked in step 2 cannot be used to add a circle tangent to it inside the boundaries of our shape, so we must go back and try to find a different $C_m$. We put back in the front any circles that we removed in step 4. We resurrect any circles that we may have killed in step 4, apart from those that we have found in step 2 while trying to find the $i$th circle. We kill $C_m$ and we return to step 2.
-
If it does not, we insert $C_i$ in the front and we return to step 2 to insert the next circle ($i \leftarrow i + 1$), resurrecting all the circles in the front.
-
Steps 2–5 are repeated until we have inserted the desired number of circles or we cannot add a circle because there is no circle left alive in the front.
Let's delve a bit deeper in what is going on with circles that are alive, dead, and resurrected. When we try to add a circle $C_i$ with a given radius, we find the circle in the front, $C_m$, that is closest to our starting point. The tangent circle that we try to add can intersect with the front, so we then need to adjust the front. The circles we remove from the front are no longer alive. After doing that, however, we may discover that our efforts have been in vain, because the tangent circle hits the boundaries of our shape. Then we should not have picked that $C_m$ in the first place and we should not have adjusted the front. Circle $C_m$ must remain dead, as well as any previous $C_m$ circles that we may have tried in our effort to insert $C_i$ in the shape; all other circles that we killed by adjusting the front must be resurrected. When finally we do manage to insert $C_i$ somewhere, we will continue to add circle $C_{i+1}$; when we begin our effort to insert a new circle, we must start fresh, by having all the circles in the front alive.
As for the resurrection itself, in reality this is but an implementation of an undo functionality. When we undo our actions, we reverse them from the most recent to the previous ones, going backwards in time; that is, we use a Last In First Out (LIFO) logic.
Roundings
Let's take three circles with radii equal to $1$, as in the following figure. $C_1$ is centered at $(0, 0)$, $C_2$ at $(2, 0)$, and $C_3$ at $(1, \sqrt{3})$; $C_3$ is tangent to $C_1$ and $C_2$ and the coordinates of its center can be found using the Pythagorean theorem. What is the distance between the centers of $C_1$ and $C_2$ and between $C_1$ and $C_3$? Both distances are equal to $2$, as all the radii are equal.
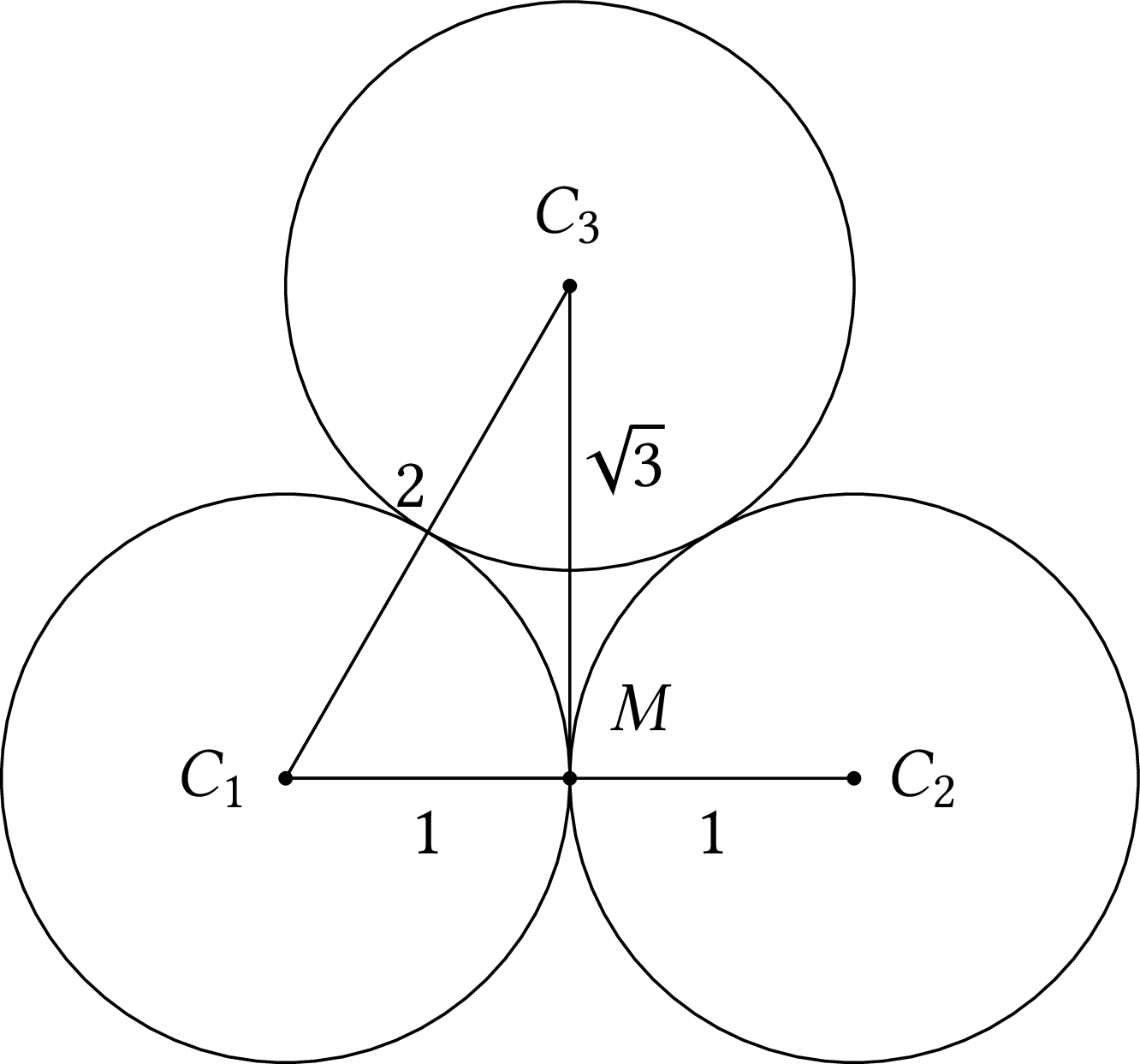
Suppose now that from the coordinates of $C_1$ and $C_3$ we want to calculate anew the distance $C_1 C_3$. Using the Pythagorean theorem again, this distance will be equal to $\sqrt{(\sqrt{3})^2 + 1^2} = 2$. If, however, we carry out the calculation in our computer, we will find that the result is $1.999\ldots < 2$.
This happens because real (floating point) numbers are stored in a computer with a specific precision; therefore, irrational numbers are not stored exactly and calculations involving irrational numbers will produce different results than what we would expect from theory. In this assignment, you should use roundings to avoid surprises:
-
Round the distance from the center of a circle to the starting point.
-
Once we calculate the coordinates of the center of a new circle, round the coordinates.
-
When you check whether two circles intersect, you must check whether the distance of their centres is greater than the sum of their radii. Round that distance before making the comparison.
-
Round the distance of a circle from a line segment.
Round the numbers to two decimal places. If you do that, your program would find that in the previous figure, the distance $C_1 C_3$ is equal to the distance $C_1 C_2$.
Having said that, rounding to two decimal places means losing precision, so again your calculations may not be what theory would predict. But at least you will know where any discrepancies come from.
Finding the Circle Closest to the Starting Point
If $(x, y)$ are the coordinates of the starting point, then to find the circle in the front that is closest to the starting point, we need to find the distances of the centers of the front's circles to the starting point. For every circle in the front with center at $(m_x, m_y)$, the distance is:
$$ d = \sqrt{(m_x - x)^2 + (m_y - y)^2} $$
If $(x, y) = (0, 0)$, then we have:
$$ d = \sqrt{m_{x}^2 + m_{y}^2} $$
For simplicity we will be using $(0, 0)$ as our starting point.
Finding a Circle Tangent to Two Other Circles
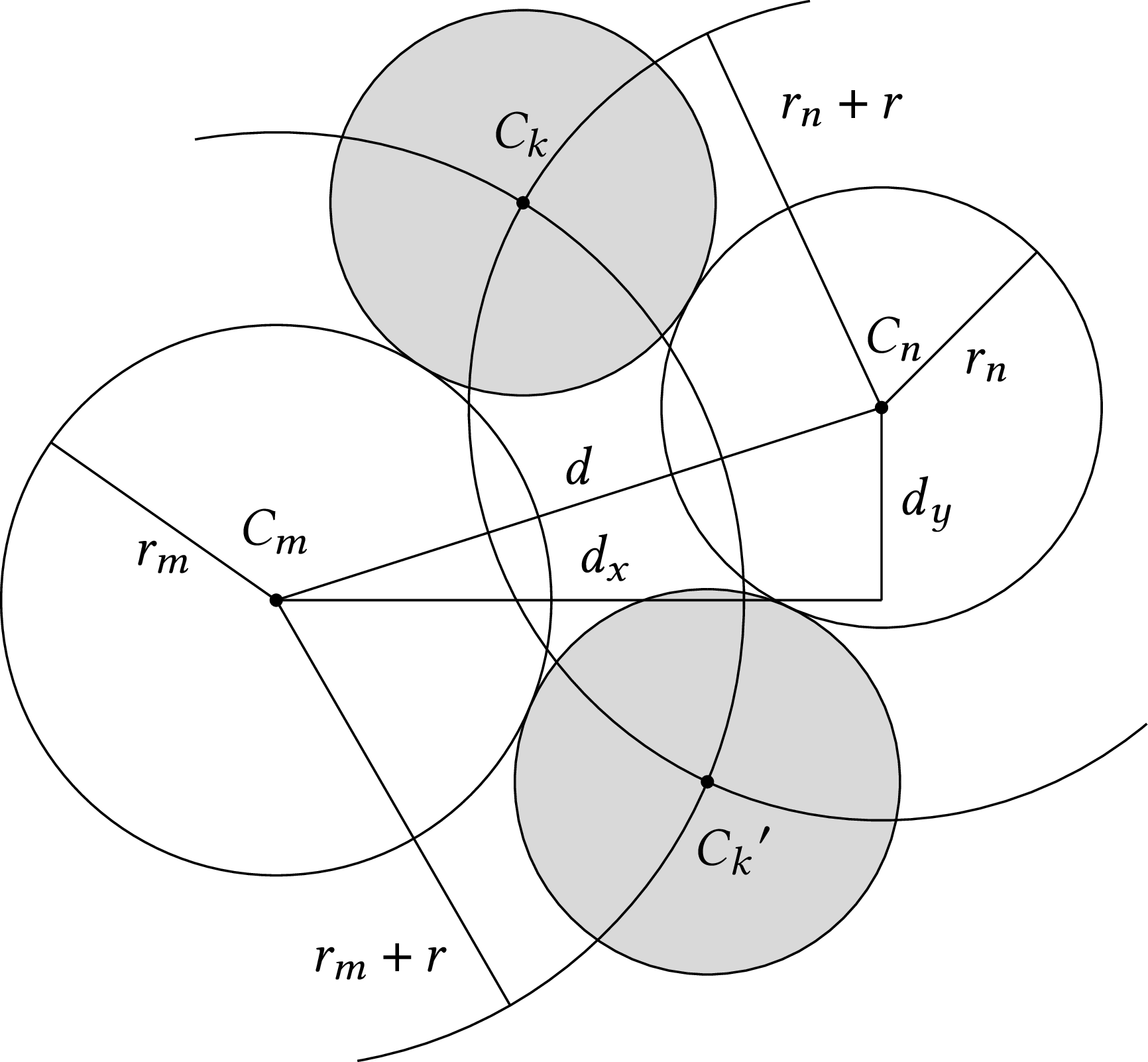
If we have two circles $C_m$ and $C_n$ and we want to find a third circle $C_k$, wih radius $r$, tangent to these two, as in the following figure, we work as follows:
-
We calculate the horizontal distance $d_x$ and the vertical distance $d_y$ of the two circles $C_m$ and $C_n$. If $(m_x, m_y)$ is the center of $C_m$ and $(n_x, n_y)$ is the center of $C_n$, we have: $$d_x = n_x - m_x$$ $$d_y = n_y - m_y $$
-
We calculate the distance between the centers of $C_m$ and $C_n$; $$ d = \sqrt{d{_x}^2+ d{_y}^2}$$
-
If $r_m$ is the radius of $C_m$ and $r_n$ is the radius of $C_n$, we calculate: $$r_1 = r_m + r $$ $$r_2 = r_n + r $$
-
We find: $$\lambda = \frac{r{_1}^2 - r{_2}^2 + d^2}{2 d^2}$$ $$\varepsilon = \sqrt{\frac{r{_1}^2}{d^2} - \lambda^2}$$
-
The center $(k_x, k_y)$ of circle $C_k$ is: $$k_x = m_x + \lambda d_x \mp \varepsilon d_y $$ $$k_y = m_u + \lambda d_y \pm \varepsilon d_x $$
-
We observe that we have two centers. We will use the first of them (that is, $- \varepsilon d_y$ for $k_x$ and $+ \varepsilon d_x$ for $k_y$). Then the circles will be added to our shape counter-clockwise, as in our examples.
If we had a ruler and a compass, it would be easy to find the tangent circles with a simple geometrical construction. In the figure you can see that it suffices to find the intersection points $C_m$ and $C_n$ with radii $r_m + r$ and $r_n + r$ respectively. The mathematical formulas above are derived using vector analysis.
Distance of Circle from Line Segment
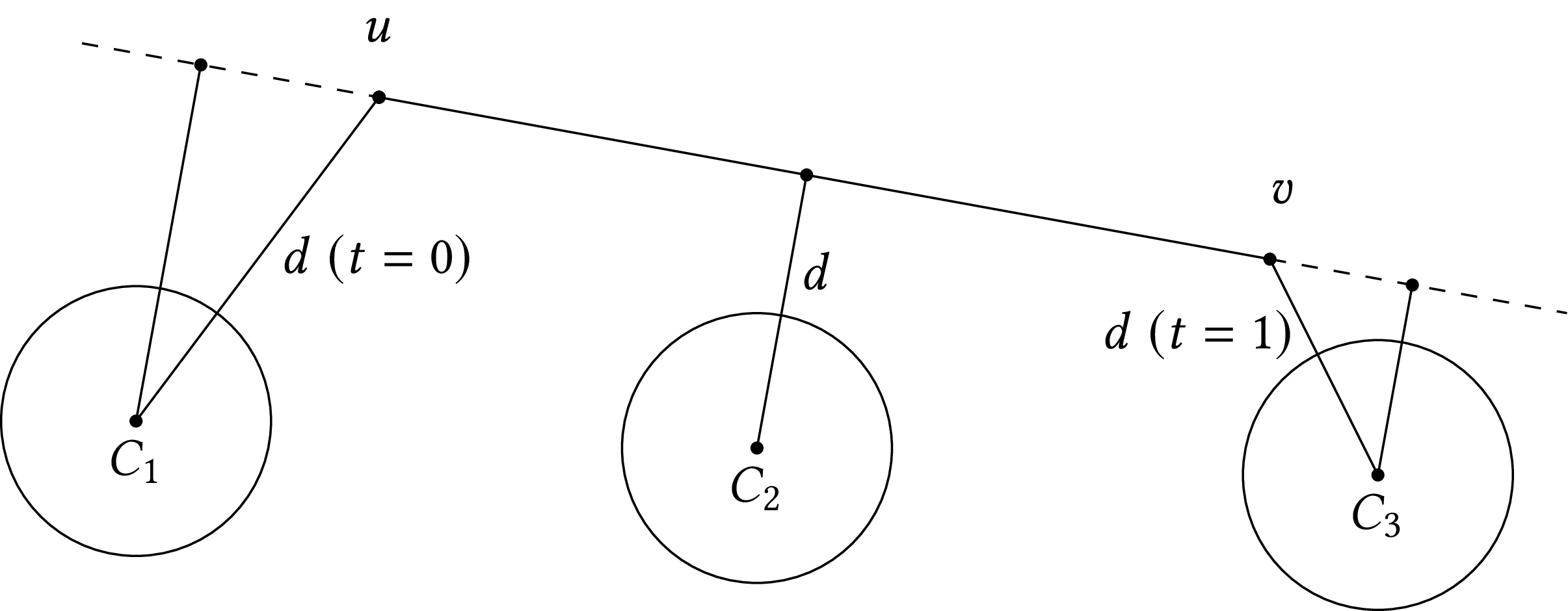
To find the distance of a circle from a line segment that lies between two points $u$ and $v$, we must first find the distance of the center of the circle from the segment. If the circle's center has coordinates, $(c_x, c_y)$, we go like this:
-
We calculate the square of the distance between the two points: $$ l_2 = (u_x - v_x)^2 + (u_y - v_y)^2$$
-
If this distance is equal to zero, then the two endpoints of the segment coincide, therefore the distance from the center of the circle is simply: $$d = \sqrt{(u_x - c_x)^2 + (u_y - c_y)^2}$$
-
Otherwise, we calculate: $$ t = \frac{(c_x - u_x) (v_x - u_x) + (c_y - u_y) (v_y - u_y)}{l_2}$$
-
We make sure that $t$ is between $0$ and $1$: $$t = \max(0, \min(1, t))$$
-
We find the projection $p$ of the center of the circle on the line segment: $$ p_x = u_x + t (v_x - u_x) $$ $$ p_y = u_y + t (v_y - u_y) $$
-
The distance of the center from the segment is: $$d = \sqrt{(p_x - c_x)^2 + (p_y - c_y)^2}$$
The above hold beause if we have two points $u$ and $v$, the straight line passing through these two points is given by the parametric equations:
$$ x = u_x + t(v_x - u_x) $$ $$ y = u_y + t(v_y - u_y) $$
The projection of a point $p$ on the line uses the initial value of $t$. However, the projection may lie beyond the limits of the line segment, as you can see in the following figure. The projection of the centre of left circle falls to the left of the segment, so we take the distance of the centre from $u$ by using $t = 0$. The projection of the centre of the middle circle falls inside the segment so no adjustment of $t$ is needed. In way symmetric to the left circle, the projection of the center of the right circle lies to the right of the segment, so we take the distance of the centre from $v$ by using $t = 1$. Then, we calculate the distance of the centre of the circle from the projection.
Having found the distance of the circle's center from the line segment, to find the distance of the circle from the segment we subtract the circle's radius. Or, to find whether the circle intersects the segment, we compare the distance from the centre with the radius.
Requirements
You will write a program called social-distancing.py. You may use
the standard Python libraries math, random, argparse, and sys,
but not any others. Your program will be called as follows:
python social_distancing.py [-items ITEMS]
[-r RADIUS]
[--min_radius MIN_RADIUS]
[--max_radius MAX_RADIUS]
[-b BOUNDARY_FILE]
[-s SEED]
output_file
The meaning of the program arguments is:
-
-i ITEMS,--items ITEMS: the number of items (circles) that we want to insert. If given, the program will try (but may not be able to) insert that many circles. -
-r RADIUS,--radius RADIUS: the circles radii. If given, all circles will have the same radius. -
--min_radius MIN_RADIUS: the minimum radius. If given, circles will have random radii not smaller thanMIN_RADIUS. This argument must be used with--max_radius. -
--max_radius MAX_RADIUS:: the maximum radius. If given, circles will have random sizes no bigger thanMAX_RADIUS. This argument must be used with--min_radius. -
-b BOUNDARY_FILE,--boundary_file BOUNDARY_FILE: the boundaries of the shape we want to fill. If given, the program will try to place the circles inside the given shape. -
-s SEED,--seed SEED: if given the seed for the pseudo-random genereation; you should userandom.seed(SEED)at the beginning of your program. -
output_file: the file where the results of the program will be stored; this is a mandatory argument.
When the program finishes, it will print on its output an integer
number, the number of circles it managed to insert. The circles
themselves will be saved in output_file, one in each line, in the
following format:
x y r
That is, each line contains three real numbers, the $x$ coordinate of the circle's center, the $y$ coordinate of the circle's center and its radius $r$. The numbers must be given with two decimal places.
If boundaries are given through -b BOUNDARY_FILE, the value of
BOUNDARY_FILE will be the name of a file that specifies the borders.
The file will contain lines of the form:
x1 y1 x2 y2
That is, each line will contain two coordinate pairs defining a line
segment. Your program will then include these lines, in the order they
are read, at the end of output_file, after the produced circles.
To visualize your results, you may use the following programs:
-
svg_draw.py
which you call with:
bash python svg_draw.py input_file output_file
whereinput_fileis the output file of your program andoutput_filewill be an SVG file. You will need to install thesvgwritelibrary. -
mpl_draw.py
which you call with:
bash python mpl_draw.py input_file output_file
whereinput_fileis the output file of your program andoutput_fileis a file whose type is determined by its suffix. For example, if you specifymyfile.pngasoutput_fileyou will get a PNG image; if you specifymyfile.svgyou will get an SVG image; if you specifymyfile.pdfyou will get a PDF image, and so on. You will need to install thematplotliblibrary.
Examples
Example 1
If you invoke the program with:
python social_distancing.py -i 11 -r 10 circles_equal_11.txt
then the program will print 11 and it will store its results in file
circles_equal_11.txt.
This file corresponds to the second figure we have seen above.
Example 2
If you invoke the program with:
python social_distancing.py -i 1000 -r 10 circles_equal_1000.txt
then the program will print 1000 and will store its results in file
circles_equal_1000.txt. You can see the
circles in the figure below, along with the front; the last circle is
painted orange (on the right, a bit below the middle).
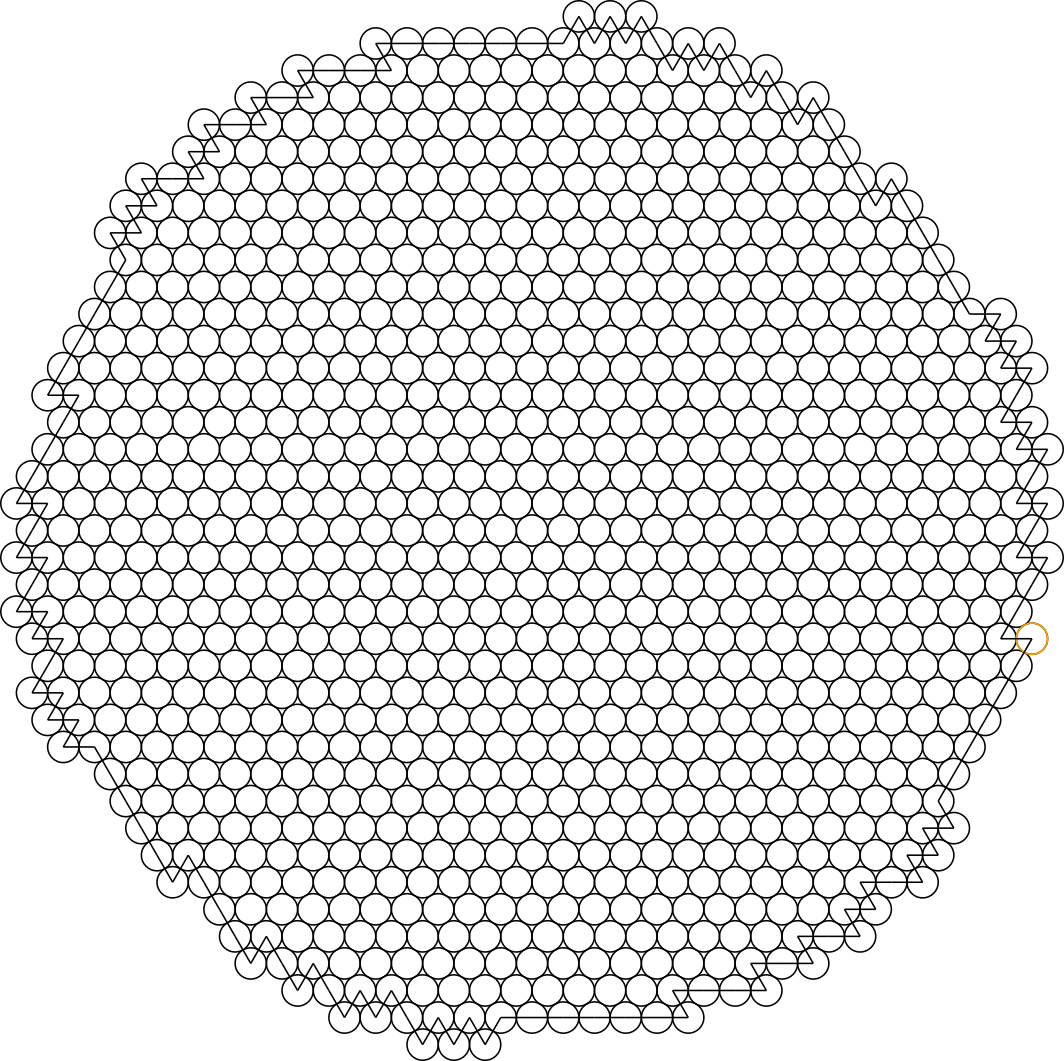
Example 3
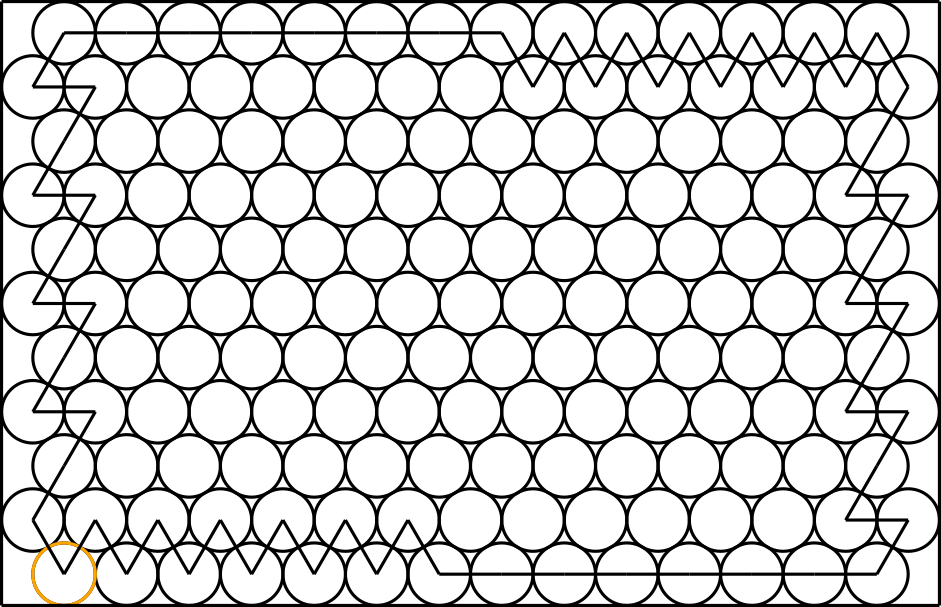
If you invoke the program with:
python social_distancing.py -i 200 -r 10 -b rectangle.txt \
circles_rectangle_equal.txt
then the program will use rectangle.txt to define
the boundaries, it will print 159 and it will store its results in
circles_rectangle_equal.txt. You can
see the circles below.
Example 4
If you invoke the program with:
python social_distancing.py -i 1000 --seed 13 \
--min_radius 5 --max_radius 10 circles_random_1000.txt
then the program will print 1000 and it will store its results in
circles_random_1000.txt. You can see the
corresponding image below.

Example 5
If you invoke the program with:
python social_distancing.py --seed 42 \
--min_radius 5 --max_radius 10 -b square_holes.txt \
square_holes_random.txt
Then the program will use
square_holes.txt to define the boundaries, it
will print 584 and it will store its results in
square_holes_random.txt. This file
corresponds to the following figure.

Notes
- The proof for the formulas for finding tangent circles is in 1.12.2 and 3.12.2 of [1]. The proof for finding the distance of a point from a line segment comes from 1.11.12 και 3.11.10 of the same book and https://stackoverflow.com/a/1501725.
- The algorithm described in the assignment for filling the plane without boundaries was published in [2].
- The problem is a special case of circle packing, which has attracted the attention of mathematicians for centuries. You can find some details at the Wikipedia article.
- The modified algorithm for filling the circles in a defined shape is not designed to be optimal; however, it differs from simple circle packing because it is an online algorithm. It tries to pack as many circles as possible in a given space, while having to place each circle as it comes, and without having the opportunity to move a set circle to another place. It therefore solves social distancing when we have to place people as they come, people may have different space requirements around them, and we cannot move people once we have put them in their position.
Bibliography
- John Vince. Geometry for Computer Graphics: Formulae, Examples & Proofs. Springer, 2005. ↩
- Weixin Wang, Hui Wang, Guozhong Dai, and Hongan Wang. Visualization of large hierarchical data by circle packing. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, CHI ’06, 517–520. New York, NY, USA, 2006. Association for Computing Machinery. URL: https://doi.org/10.1145/1124772.1124851, doi:10.1145/1124772.1124851. ↩
