Real World Algorithms

The best known work of the Irish writer Samuel Beckett (1906–1989, Nobel prize in Literature 1969) is the play "Waiting for Godot". Beckett, who lived in Paris for the largest part of his life, wrote it first in French in 1952 ("En attendant Godot") and then in English in 1954. In the play, the two main characters, Vladimir and Estragon, are, per the title, waiting for Godot. We don't know why. While waiting they talk and meet with others. The play ends but Godot has not come. They will continue to wait for him.

In this assignment we will deal with another one, lesser known play by Beckett, written for the television. In this play, called "Quad", there are four characters. Beckett wanted them to appear on stage with a specific way. Only one character may enter or exit at a certain point and the character who exits must be the one that has been on stage the longest. Moreover, Beckett wanted all possible combinations of the four characters to appear in the play exactly once.

He was not able to find a way to do that. Indeed, it is impossible to achieve such a sequence of entrances and exits for four characters without repeating some of the combinations.

Let us now return to Computer Science. The Gray code with $n$ bits is a cyclical ordering of the binary numbers with $n$ bits so that two successive values differ by one bit. For instance, the Gray code for $n = 4$ is:

0000, 0001, 0011, 0010, 0110, 0111, 0101, 0100, 1100, 1101, 1111, 1110, 1010, 1011, 1001, 1000.

Note that each number differs both from the previous one and the following one by a single bit. Also, this holds for the first and last items in the sequence if we take the first item to follow the last item, so that the code is cyclical.

It is easy to construct such a code with $n$ bits, working recursively. If by $\Gamma_n$ we denote the Gray code with $n$ bits and $\Gamma_0$ is the empty string, then to construct the Gray code with $n+1$ bits we only need to take the Gray code with $n$ bits, prefix each string with $0$, reverse it, and then prefix each string of the reversed sequence with $1$. Indeed:

$$\Gamma_1 = 0, 1$$

We just prefixed the empty string with $0$ and $1$. Then:

$$\Gamma_2 = 00, 01, 11, 10$$

We prefixed each string of $0, 1$ with $0$ and then we prefixed each string of the sequence $1, 0$ with $1$.

Similarly:

$$\Gamma_3 = 000, 001, 011, 010, 110, 111, 101, 100$$

We prefixed each string of $00, 01, 11, 10$ with $0$ and each string $10, 11, 01, 00$ with $1$.

From the way it is built, this code is called, if we want to be more precise, Reflected Binary Code (RBC), or Reflected Binary (RB).

But note that we can have a code that meets the requirement of changing a single bit each time without building it in this way. For instance, in the balanced Gray code, we want to have the same number of changes for each bit. Here is a balanced Gray code of four bits:

$$ \begin{matrix} 0 & \boxed{1} & 1 & 1 & 1 & 1 & 1 & \boxed{0} & 0 & 0 & 0 & 0 & 0 & \boxed{1} & 1 & \boxed{0}\ 0 & 0 & \boxed{1} & 1 & 1 & 1 & \boxed{0} & 0 & \boxed{1} & 1 & 1 & 1 & \boxed{0} & 0 & 0 & 0\ 0 & 0 & 0 & 0 & \boxed{1} & 1 & 1 & 1 & 1 & \boxed{0} & 0 & \boxed{1} & 1 & 1 & \boxed{0} & 0\ \boxed{0} & 0 & 0 & \boxed{1} & 1 & \boxed{0} & 0 & 0 & 0 & 0 & \boxed{1} & 1 & 1 & 1 & 1 & 1 \end{matrix} $$

Each item of the code corresponds to a column. You can verify that in each row we have four bits changing in total.

By adopting other requirements we can create different Gray codes. We can also drop the requirement for the code to be cyclical. If it is not, we say that the code is a path, but not a cycle.

If we adopt the requirement that want the bit that changes to zero to be the bit that has remained for longer with value one, then the resulting code meets the criterion set by Beckett—and, therefore, it is a Beckett-Gray code.

For $n = 3$ there is no Beckett-Gray code, because it is not possible to find a cyclical code that meets the Beckett requirement; there is, however, a single path:

$$ \begin{matrix} 0 & \boxed{1} & 1 & \boxed{0} & 0 & 0 & \boxed{1} & 1\ 0 & 0 & \boxed{1} & 1 & 1 & \boxed{0} & 0 & \boxed{1}\ 0 & 0 & 0 & 0 & \boxed{1} & 1 & 1 & 1 \end{matrix} $$

You can verify that the bit that goes off in a column is the one that has stayed on for longest in its row.

For $n = 4$, again, there is no Beckett-Gray code, so it's no surprise that Beckett could not find one for his play. But there are four paths:

$$ \begin{matrix} 0 & \boxed{1} & 1 & \boxed{0} & 0 & 0 & 0 & 0 & \boxed{1} & 1 & 1 & 1 & 1 & \boxed{0} & 0 & \boxed{1}\ 0 & 0 & \boxed{1} & 1 & 1 & \boxed{0} & 0 & 0 & 0 & 0 & 0 & \boxed{1} & 1 & 1 & 1 & 1\ 0 & 0 & 0 & 0 & \boxed{1} & 1 & 1 & \boxed{0} & 0 & \boxed{1} & 1 & 1 & 1 & 1 & \boxed{0} & 0\ 0 & 0 & 0 & 0 & 0 & 0 & \boxed{1} & 1 & 1 & 1 & \boxed{0} & 0 & \boxed{1} & 1 & 1 & 1 \end{matrix} $$

$$ \begin{matrix} 0 & \boxed{1} & 1 & \boxed{0} & 0 & 0 & 0 & 0 & 0 & 0 & \boxed{1} & 1 & 1 & 1 & 1 & 1\ 0 & 0 & \boxed{1} & 1 & 1 & \boxed{0} & 0 & 0 & \boxed{1} & 1 & 1 & 1 & \boxed{0} & 0 & 0 & \boxed{1}\ 0 & 0 & 0 & 0 & \boxed{1} & 1 & 1 & \boxed{0} & 0 & \boxed{1} & 1 & 1 & 1 & 1 & \boxed{0} & 0\ 0 & 0 & 0 & 0 & 0 & 0 & \boxed{1} & 1 & 1 & 1 & 1 & \boxed{0} & 0 & \boxed{1} & 1 & 1 \end{matrix} $$

$$ \begin{matrix} 0 & \boxed{1} & 1 & 1 & 1 & \boxed{0} & 0 & 0 & \boxed{1} & 1 & 1 & \boxed{0} & 0 & 0 & 0 & \boxed{1}\ 0 & 0 & \boxed{1} & 1 & 1 & 1 & \boxed{0} & 0 & 0 & 0 & 0 & 0 & \boxed{1} & 1 & 1 & 1\ 0 & 0 & 0 & \boxed{1} & 1 & 1 & 1 & \boxed{0} & 0 & \boxed{1} & 1 & 1 & 1 & \boxed{0} & 0 & 0\ 0 & 0 & 0 & 0 & \boxed{1} & 1 & 1 & 1 & 1 & 1 & \boxed{0} & 0 & 0 & 0 & \boxed{1} & 1 \end{matrix} $$

$$ \begin{matrix} 0 & \boxed{1} & 1 & 1 & 1 & \boxed{0} & 0 & 0 & 0 & 0 & 0 & 0 & \boxed{1} & 1 & 1 & 1\ 0 & 0 & \boxed{1} & 1 & 1 & 1 & \boxed{0} & 0 & \boxed{1} & 1 & 1 & \boxed{0} & 0 & 0 & 0 & \boxed{1}\ 0 & 0 & 0 & \boxed{1} & 1 & 1 & 1 & \boxed{0} & 0 & 0 & \boxed{1} & 1 & 1 & 1 & \boxed{0} & 0\ 0 & 0 & 0 & 0 & \boxed{1} & 1 & 1 & 1 & 1 & \boxed{0} & 0 & 0 & 0 & \boxed{1} & 1 & 1\ \end{matrix} $$

For $n = 5$ there are 16 Beckett-Gray codes. At this point, let's introduce a more practical way to represent Gray codes and paths. As only a single bit changes each time, to represent a Gray code or path we only need to give the sequence of bits that change, where each bit is represented by its position, counting from the right. That is called delta sequence or transition sequence and we denote it with $\delta$. So, for the Gray cycle with $1$ bit we have $\delta = 00$ and for the Gray cycle with $2$ bits we have $\delta = 0101$.

Proceeding to $n = 3$, for the Gray cycle that we obtain by closing $\Gamma_3$ we have $\delta = 01020102$, while there exists also amother Gray cycle (which is not reflected) with $\delta = 01210121$.

Using delta sequences, the 16 Beckett-Gray codes for $n = 5$ are:

$$ \begin{matrix} 01020132010432104342132340412304 & 01020312403024041232414013234013\ 01020314203024041234214103234103 & 01020314203240421034214130324103\ 01020341202343142320143201043104 & 01023412032403041230341012340124\ 01201321402314340232134021431041 & 01203041230314043210403202413241\ 01203104213043421310342104302402 & 01230121430214340230341420314121\ 01230124234140231410343201434204 & 01230401231340413234202341024212\ 01230401232430423134101432014121 & 01230412320434120343014312041323\ 01234010232430124313401432014121 & 01234010232430201432014132413141\ \end{matrix} $$

Gray codes have graph interpretation and a related geometrical interpretation. If we create a graph whose vertices are the elements of the code and the edges connect two elements that differ by a single bit, then the possible paths and cycles are the various ways to explore the graph starting from a different edge of the graph. A path that covers all the vertices exactly once is called a Hamiltonian path and a cycle that visits all the vertices exactly once is called a Hamiltonian cycle. Given that each vertex has exactly $n$ neighbors, such a graph, in geometrical terms, is a hypercube. Below you can see the hypercuble for $n = 4$ and a Hamiltonian cycle on it. The Hamiltonian cycle corresponds to the reflective Gray code for $n = 4$.

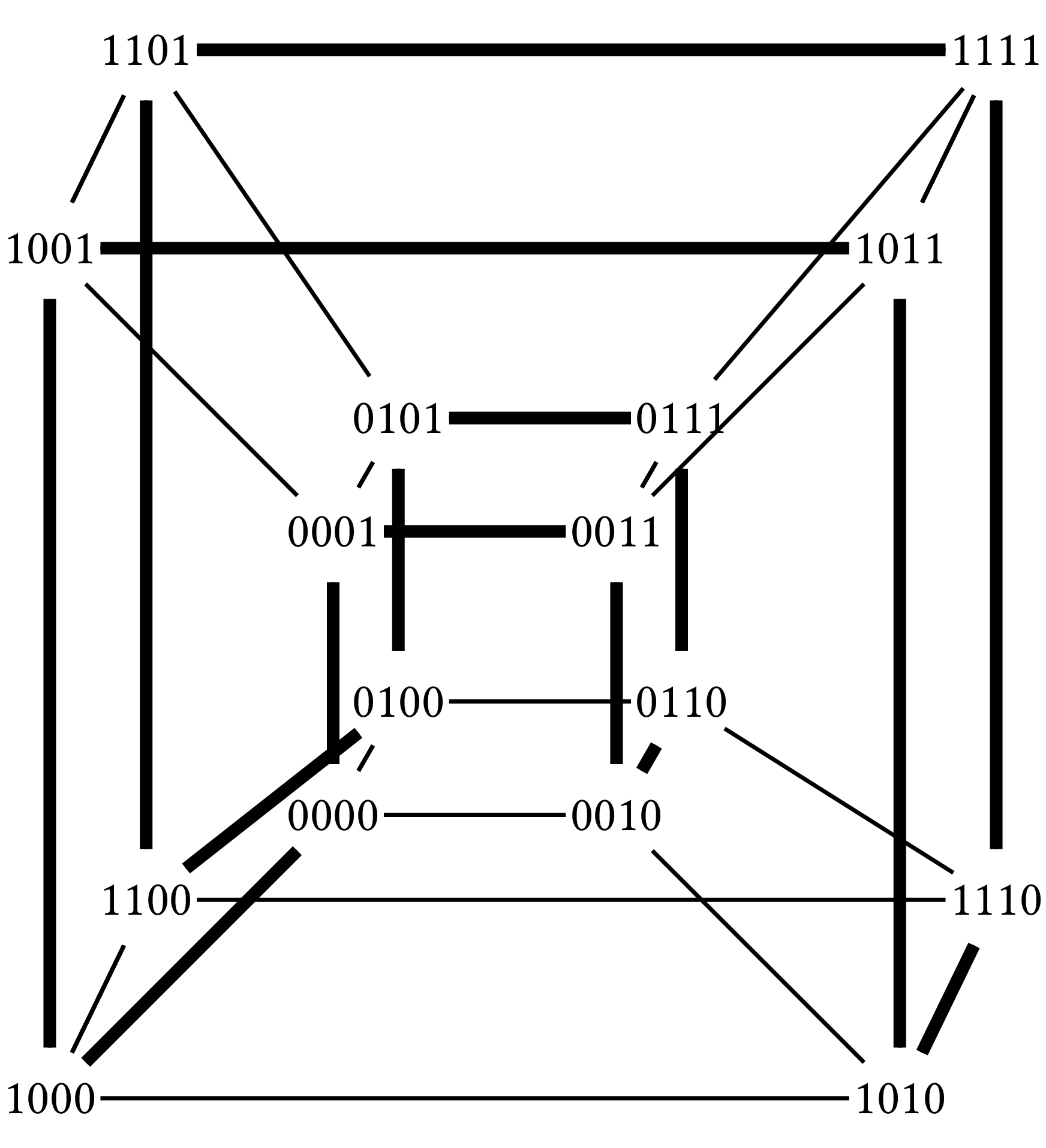
If we want to find all Gray codes, it suffices to find all paths and cycles on the corresponding graph (or hypercube). However, some of the resulting codes can be derived from other codes by just permutating the bit positions. To see that, we will need some definitions. Let us call coordinates the elements of a delta sequence: for $n=3$ the coordinates are $0, 1, 2$. We will denote by $d(n)$ the number of different delta sequences for a given $n$. We will denote by $c(n)$ the number of canonical delta sequences, in which each coordinate $k$ appears in the sequence before the first appearance of coordinate $k+1$. As every permutation of the coordinates of a delta sequence produces another delta sequence, we have $d(n) = n!c(n)$. Indeed, we saw that for $\Gamma_3$ we have $\delta = 01020102$. If we apply the permutation:

$$ \begin{pmatrix} 0 & 1 & 2\ 1 & 0 & 2 \end{pmatrix} $$

we obtain $\delta = 10121012$, which you can verify that it is a Gray code, but the delta sequence is not canonical as $1$ appears in it before $0$. If a Gray code can be obtained by another one through permutation, we say that the two codes are isomorphic. To find all the non-isomorphic Gray codes, we must ensure that when exploring the Hamiltonian paths and cycles our trail follows only canonical delta sequences.

We know that in order to explore a graph, we can use depth-first search. Here we will use a variant of depth-first search that will have the following characteristics:

• The exploration will proceed from node to node of the hypercube.

• At each node, we note the largest coordinate that we can change.

• The neighbors of the node are produced from the current node by changing a bit at a time, starting from the least significant one (the first from the right, at position zero), until the largest coordinate.

• In traditional depth-first search, we note each node that we visit so that we do not visit it again. In this way we explore the graph only once. Here, though, we want to explore the graph exhaustively, finding all possible paths that meet our requirements. That means that we must take care so that once we have explored a path we can revisit its nodes (in a different order).

We can achieve the above with the algorithm that follows. The algorithm builds Gray codes one at a time using the stack $\mathit{gc}$ and it collects them in the list $\mathit{all_codes}$, which is initially empty. To call the algorithm, we must initialize the array $\mathit{visited}$ with all its elements set to false, apart from from $\mathit{visited}[0]$ which will be set to true; the $\mathit{gc}$ stack will initially contain element $0$. The algorithm's parameters include the recursion depth, $d$, starting from $d = 1$, so that we can define the condition to stop the recursion—when we have visited all $2^n$ nodes of the hypercube. The algorithm uses function $\texttt{Flip(}x, i\texttt{)}$, which changes the value of bit $i$ in $x$. When we start $x$ is zero, while $\mathit{max_coord}$, as we don't want to use a coordinate before we use the smaller coordinates, is also zero.

This algorithm will produce all Gray codes. That is not enough for us: we want to be able to produce the Beckett-Gray codes. To achieve that, we need to modify the algorithm a little. We will use a queue to know that when we set a bit to zero, that will be the bit whose value has stayed at one for the longest time.

The algorithm ensures that we will find the codes that are not isomorphic due to permutations. We can extend the definition of isomorphism between codes to include codes that can be derived from one another via reversal, and not just permutation. For example, let's take the first Beckett-Gray code for $n = 5$ that we saw before:

$$ 01020132010432104342132340412304 $$

This code is isomorphic with:

$$ 01234010232430201432014132413141 $$

Indeed, if we reverse it, we get:

$$ 14131423141023410203423201043210 $$

But from code:

$$ 01020132010432104342132340412304 $$

we can derive code:

$$ 14131423141023410203423201043210 $$

with the permutation:

$$ \begin{pmatrix} 0 & 1 & 2 & 3 & 4\ 1 & 4 & 3 & 2 & 0 \end{pmatrix} $$

In this assignment you will write a program that will produce various kinds of Gray codes and will find any isomorphisms that can be obtained via reversals and permutations.

Requirements

You will write a program called beckectt_gray.py. You may use the following libraries: itertools, argparse or sys (in particular, the list sys.argv) to handle program arguments.

Your program will be called as follows:

python beckett_gray.py [-a | -b | -u | -c | -p] [-r] [-f] [-m] number_of_bits

The program will take the following arguments:

• -a: find all codes (cycles and paths)

• -b: find Beckett-Gray codes

• -u: find Beckett-Gray paths (not cyles)

• -c: find cyclical codes

• -p: find Gray paths

• -r: find reverse isomorphisms

• -f: show the full binary representation of each code

• -m: show each code with a tabular representation

• number_of_bits: the number of bits of the code

The meaning of the arguments is illustrated in the examples that follow.

Examples

Example 1

If you invoke the program with:

python beckett_gray.py -a 3

or simply:

python beckett_gray.py 3

the program will produce the following output:

C 01020102
P 0102101
C 01210121

It found three codes, presented with their delta sequences. Two of the codes are cyclical (prefixed with C) and one is a path (prefixed with P).

Example 2

If you invoke the program with:

python beckett_gray.py -b 5

the program will produce the following output:

B 01020132010432104342132340412304
B 01020312403024041232414013234013
B 01020314203024041234214103234103
B 01020314203240421034214130324103
B 01020341202343142320143201043104
B 01023412032403041230341012340124
B 01201321402314340232134021431041
B 01203041230314043210403202413241
B 01203104213043421310342104302402
B 01230121430214340230341420314121
B 01230124234140231410343201434204
B 01230401231340413234202341024212
B 01230401232430423134101432014121
B 01230412320434120343014312041323
B 01234010232430124313401432014121
B 01234010232430201432014132413141

that is, it found 16 Beckett-Gray codes (prefixed with B).

Example 3

If you invoke the program with:

python beckett_gray.py -b 5 -r

the program will output the contents of the file bgc_5_isomorphic.txt that is, as in the previous example, but adding in the end the reversed isomorphisms.

Example 4

If you invoke the program with:

python beckett_gray.py -c 4

the program will output the contents of the file gc_4_cycles.txt.

Example 5

If you invoke the program with:

python beckett_gray.py -u 3

the program will output:

U 0102101

that is, a path (the only one for $n = 3$) that fulfils Beckett's requirement, hence the prefix U (unfinished, as it ends without closing the cycle).

Example 6

If you invoke the program with:

python beckett_gray.py -u 4

the program will produce the following output:

U 010213202313020
U 010213212031321
U 012301202301230
U 012301213210321

Example 7

If you invoke the program with:

python beckett_gray.py -b -f 5

the program will output the contents of the file bgc_5_full.txt; that is, except from the delta sequence, it will also output the full binary representation of each code.

Example 8

If you invoke the program with:

python beckett_gray.py -u -m 4

the program will output:

U 010213202313020
0 1 1 0 0 0 0 0 1 1 1 1 1 0 0 1
0 0 1 1 1 0 0 0 0 0 0 1 1 1 1 1
0 0 0 0 1 1 1 0 0 1 1 1 1 1 0 0
0 0 0 0 0 0 1 1 1 1 0 0 1 1 1 1
U 010213212031321
0 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1
0 0 1 1 1 0 0 0 1 1 1 1 0 0 0 1
0 0 0 0 1 1 1 0 0 1 1 1 1 1 0 0
0 0 0 0 0 0 1 1 1 1 1 0 0 1 1 1
U 012301202301230
0 1 1 1 1 0 0 0 1 1 1 0 0 0 0 1
0 0 1 1 1 1 0 0 0 0 0 0 1 1 1 1
0 0 0 1 1 1 1 0 0 1 1 1 1 0 0 0
0 0 0 0 1 1 1 1 1 1 0 0 0 0 1 1
U 012301213210321
0 1 1 1 1 0 0 0 0 0 0 0 1 1 1 1
0 0 1 1 1 1 0 0 1 1 1 0 0 0 0 1
0 0 0 1 1 1 1 0 0 0 1 1 1 1 0 0
0 0 0 0 1 1 1 1 1 0 0 0 0 1 1 1

that is, underneath each code it will include its representation in matrix format.

In his penultimate novella, "Westward Ho", Samuel Beckett wrote what may be his most famous phrase:

Ever tried. Ever failed. No matter. Try again. Fail again. Fail better.

Notes

Our description of Gray codes follows [2], section 7.2.1.1. Gray codes were named after Frank Gray, a physist that invented $\Gamma_n$ for the analog transmission of digital signals; however Gray codes existed before that. Knuth traces them back to 1878, when $\Gamma_5$ were used by Émile Baudot in a telegraph machine. The term "baud", named after him, is a unit of transmission equalling the number of times a signal changes per second. Knuth also points out that Gray codes underlie the Baguenaudier or Chinese ring puzzle. The algorithm we present here is adapted from [3]; see [1] for a more recent treatment.

Bibliography