In Arthur C. Clarke's book Imperial Earth, the main character has to solve two problems with pentominoes. A pentomino is a polygon that is made up from five equal square tiles placed such that every two tiles share one side. There are 12 different pentominoes if we do not take into account rotations and reflections:
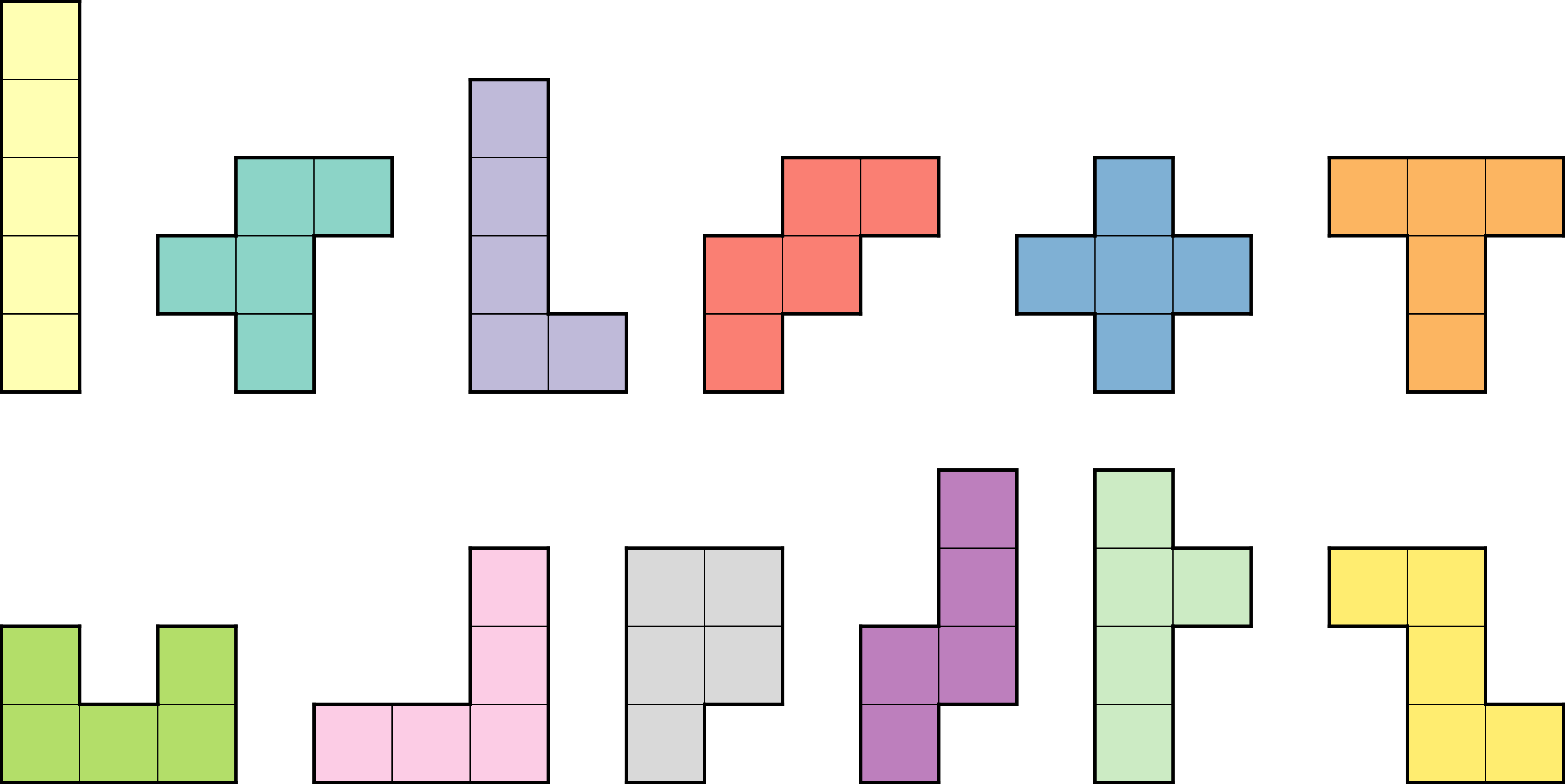
The two problems in the book were:
-
Can we fill a rectangle with dimensions $6\times 10$ using these 12 pentominoes? It turns out that the answer is yes, and there are 2339 different solutions. Here is one of them:

-
Can we fill a rectangle with dimensions $3\times 20$ using these 12 pentominoes? Again, it turns out that the answer is yes, but there are only two solutions. Here is one of them:

As you can see, the pentominoes in these rectangles can be rotated or reflected, horizontally or vertically. But if we do such transformations, how many different shapes can we produce?
If we allow a pentomino to be transformed, then we no longer have only 12 possible shapes. For example, take the pentomino:

If we rotate it or reflect it, we can get the following eight shapes:
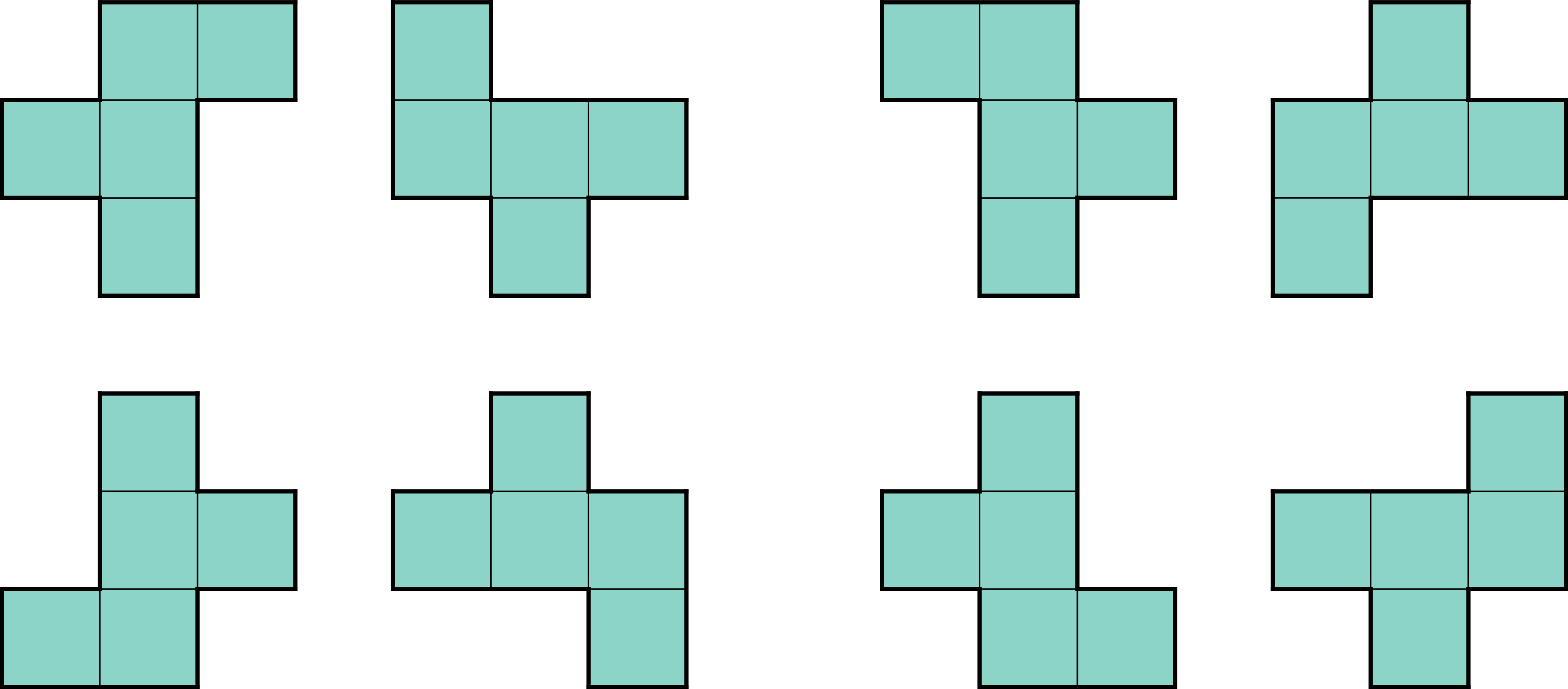
In total, there are 63 different pentominoes if we allow rotations and reflections. When rotations and reflections are not allowed, we call the set of pentominoes we have free; these are the 12 pentominoes we saw at the beginning. Otherwise, if rotations and reflections are allowed, we have 63 fixed pentominoes.
We can now generalize and work with a different number of tiles instead of five. A polyomino is a geometrical shape consisting of a number of square tiles, with each two of them sharing a side. As in pentominoes, polyominoes can be fixed or free. We are interested in finding a way to count the number of fixed polyominos, for every possible number of tiles $n$.
To find that count, we can work as follows. We will take pentominoes as our example. We create a square lattice, on which we will place the pentominoes. All pentominoes will be placed so that they cover tile $(0, 0)$. Given that, the pentominoes may extend to the grayed tiles of the following shape:

The bold line indicates the tiles whose coordinates are:
$$ {\, (x, y)\ |\ (y >0)\ \mathrm{or}\ (y = 0)\ \mathrm{and}\ x \ge 0 \,} $$
Then, to find the different pentominoes, we take five tiles such that every two of them share an edge and one of them covers $(0, 0)$.
Now, let's define a graph where each node is one of the grayed tiles and its neighbors are the adjacent squared tiles:

Then, the pentominoes are the connected subgraphs of the graph that contain five nodes.
It follows that to find how many pentominoes there are, we have to find the number of connected subgraphs having five nodes. In general, if we have polyominoes of size $n$, the logic remains the same. We construct the corresponding graph and we count the number of connected subgraphs with $n$ nodes. To find these subgraphs, we can use the following algorithm:
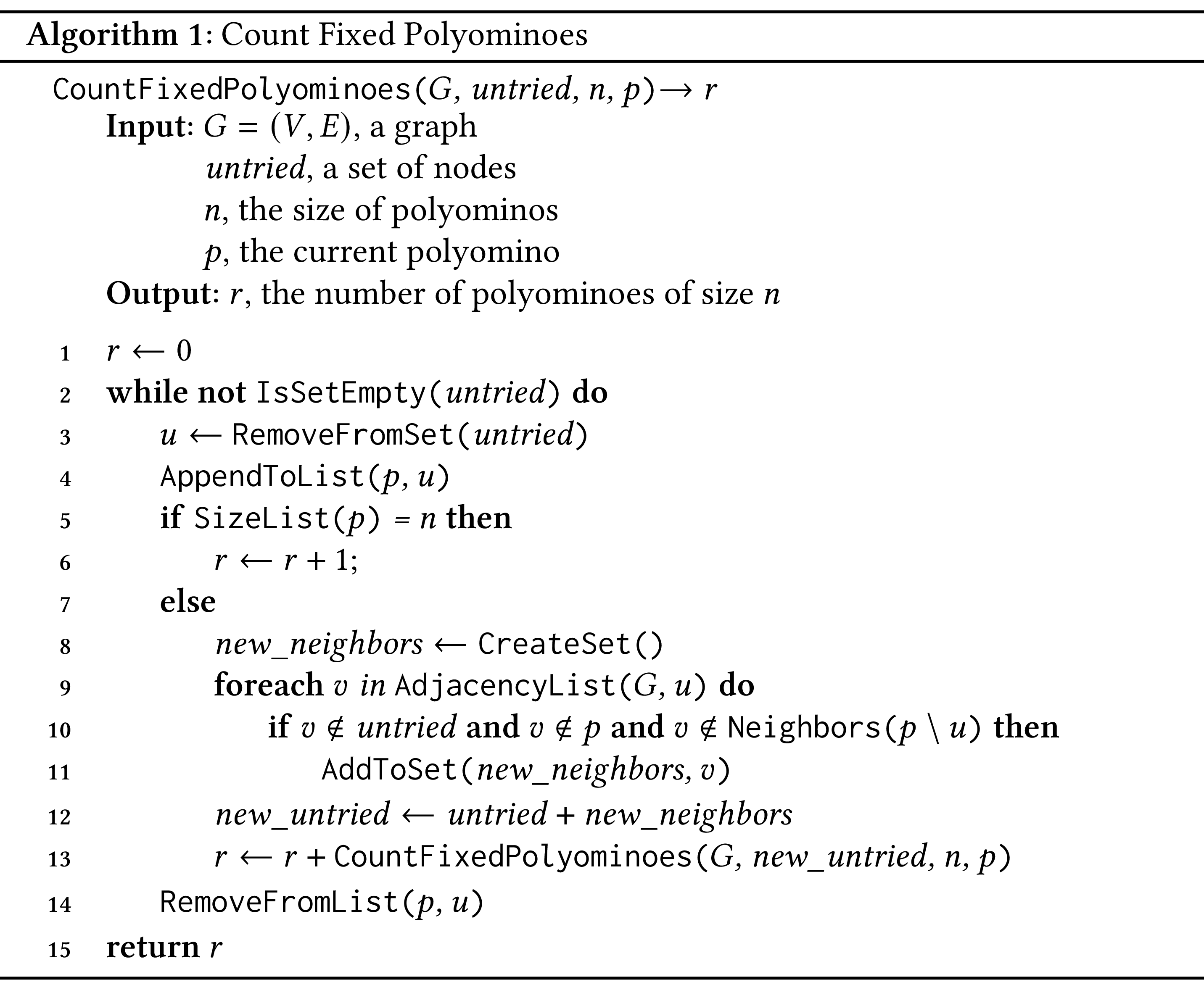
The algorithm is recursive. It takes as arguments the graph that we have constructed ($G$), a set of tiles that we need to try ($\mathit{untried}$), the size of the polyomino ($n$) and the current polyomino under construction ($p$). We call the algorithm passing as $\mathit{untried}$ the set ${(0, 0)}$ and as the current polyomino $p$ an empty list.
When we start, we initialize the counter representing the number of polyominoes to zero (line 1). The algorithm executes as long as the set $\mathit{untried}$ is not empty. We take out one element from the set, that is, a node that we call $u$ (line 3), and we add it to the current polyomino (line 5). If the current polyomino has size equal to $n$, we increase the counter by one (lines 5–6). Otherwise, in lines 8–13 we find the neighbors of $u$ for which the following hold:
-
The do not belong to set $\mathit{untried}$.
-
They do not belong in the current polyomino under construction.
-
They are not neighbors of the other nodes, apart from $u$, that belong to $p$: by $p \setminus u$ we done the nodes of $p$ apart from $u$. At this point you may wonder: “Well, $\mathit{untried}$ does contain the neighbors of the polyomino under construction, right? Why do we need this check since we already check that $v \notin \mathit{untried}$?”. The answer is no, it does not necessarily contain all the neighbors of the polyomino under construction, because each time we go through line 3 we remove an element from $\mathit{untried}$, so a neighbor may be one of the removed elements.
When we find these neighbors we create a new set of tiles that we must try (line 12) and we call the graph recursively (line 13). When the recursive call returns, we add to the counter the value returned from the call. Before the next iteration of the loop of lines 2–14, we remove node $u$ from $p$.
Requirements
You will write a program called count_fixed_polyominoes.py. Your
program will be called as follows:
python count_fixed_polyominoes.py [-p] n
The program will construct and count all fixed polyominoes of size n
and print out their number. If the user passes -p, the program will
also output the graph that is constructed. In your program:
-
You should represent the graph using adjacency lists, not the adjacency matrix.
-
If
-pis given, the nodes in the adjacency lists will have to be printed out in counter-clockwize order; see the examples below. -
You can use the
pprintlibrary for printing the graph and theargparseorsyslibrary for handling the program arguments.
Examples
Example 1
If the program is called with:
python count_fixed_polyominoes.py -p 3
the program will output:
{(-1, 1): [(0, 1)],
(0, 0): [(1, 0), (0, 1)],
(0, 1): [(1, 1), (0, 2), (-1, 1), (0, 0)],
(0, 2): [(0, 1)],
(1, 0): [(2, 0), (1, 1), (0, 0)],
(1, 1): [(0, 1), (1, 0)],
(2, 0): [(1, 0)]}
6
Example 2
If the program is called with:
python count_fixed_polyominoes.py -p 4
the output will be:
{(-2, 1): [(-1, 1)],
(-1, 1): [(0, 1), (-1, 2), (-2, 1)],
(-1, 2): [(0, 2), (-1, 1)],
(0, 0): [(1, 0), (0, 1)],
(0, 1): [(1, 1), (0, 2), (-1, 1), (0, 0)],
(0, 2): [(1, 2), (0, 3), (-1, 2), (0, 1)],
(0, 3): [(0, 2)],
(1, 0): [(2, 0), (1, 1), (0, 0)],
(1, 1): [(2, 1), (1, 2), (0, 1), (1, 0)],
(1, 2): [(0, 2), (1, 1)],
(2, 0): [(3, 0), (2, 1), (1, 0)],
(2, 1): [(1, 1), (2, 0)],
(3, 0): [(2, 0)]}
19
Example 3
If the program is called with:
python count_fixed_polyominoes.py -p 5
the output will be:
{(-3, 1): [(-2, 1)],
(-2, 1): [(-1, 1), (-2, 2), (-3, 1)],
(-2, 2): [(-1, 2), (-2, 1)],
(-1, 1): [(0, 1), (-1, 2), (-2, 1)],
(-1, 2): [(0, 2), (-1, 3), (-2, 2), (-1, 1)],
(-1, 3): [(0, 3), (-1, 2)],
(0, 0): [(1, 0), (0, 1)],
(0, 1): [(1, 1), (0, 2), (-1, 1), (0, 0)],
(0, 2): [(1, 2), (0, 3), (-1, 2), (0, 1)],
(0, 3): [(1, 3), (0, 4), (-1, 3), (0, 2)],
(0, 4): [(0, 3)],
(1, 0): [(2, 0), (1, 1), (0, 0)],
(1, 1): [(2, 1), (1, 2), (0, 1), (1, 0)],
(1, 2): [(2, 2), (1, 3), (0, 2), (1, 1)],
(1, 3): [(0, 3), (1, 2)],
(2, 0): [(3, 0), (2, 1), (1, 0)],
(2, 1): [(3, 1), (2, 2), (1, 1), (2, 0)],
(2, 2): [(1, 2), (2, 1)],
(3, 0): [(4, 0), (3, 1), (2, 0)],
(3, 1): [(2, 1), (3, 0)],
(4, 0): [(3, 0)]}
63
Example 4
If the program is called with:
python count_fixed_polyominoes.py 10
the output will be:
36446
Example 5
If the program is called with:
python count_fixed_polyominoes.py 15
the output will be:
27394666
Other Examples
For polyominoes of sizes up to and including 15, their number is as in the following table:
| Polyomino Size | Number of Fixed Polyominoes |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 19 |
| 5 | 63 |
| 6 | 216 |
| 7 | 760 |
| 8 | 2725 |
| 9 | 9910 |
| 10 | 36446 |
| 11 | 135268 |
| 12 | 505861 |
| 13 | 1903890 |
| 14 | 7204874 |
| 15 | 27394666 |
Notes
-
Arthuc C. Clarke learned about polyominoes from director Stanley Kubrick during the shooting of 2001: A Space Odyssey; he then wove them into his book [2].
-
The algorithm that you have to implement in this assignment was invented by D. Hugh Redelmeier [7].
-
The Redelmeier algorithm is not fast, as it has exponential complexity. The fast algorithm we know, although it still has exponential complexity, was invented by Iwan Jensen [6]
-
We can frame the problem in three or more dimensions; for details, see [1].
-
The term “polyomino” was introduced by Solomon W. Golomb in 1954. For more details, see his book [5].
-
Polyominoes were introduced to the wider public by Martin Gardner in 1957 and 1960 in his Scientific American column [3][4].
Bibliography
- Gadi Aleksandrowicz and Gill Barequet. Counting d-dimensional polycubes and nonrectangular planar polyominoes. In Proceedings of the 12th Annual International Conference on Computing and Combinatorics, COCOON '06, 418–427. Berlin, Heidelberg, 2006. Springer-Verlag. URL: https://doi.org/10.1007/11809678_44, doi:10.1007/11809678_44. ↩
- Arthur C. Clarke. Imperial Earth. Gollancz, London, UK, 1965. ↩
- Martin Gardner. More about complex dominoes. Scientific American, 197(6):126–140, 1957. ↩
- Martin Gardner. More about the shapes that can be made with complex dominoes. Scientific American, 203(5):186–201, 1960. doi:10.1038/scientificamerican1160-186. ↩
- Solomon W. Golomb. Polyominoes. Princeton University Press, Princeton, NJ, 2nd edition, 1994. ↩
- Iwan Jensen. Enumerations of lattice animals and trees. Journal of Statistical Physics, 102(3/4):865–881, 2001. doi:10.1023/A:1004855020556. ↩
- D. Hugh Redelmeier. Counting polyominoes: yet another attack. Discrete Mathematics, 36(2):191–203, 1981. ↩
