Real World Algorithms

Sometimes we want to break apart a set of entities to subsets such that the entities in each subset have no relationship between them. If we use a graph to represent the entities and their relationships, the problem we have to solve is to find subsets of the graph so that the members of each subset are not neighbours with any other member of the same subset. This is an instance of an independent set: a set of nodes such that no node is a neighbour of any other node in the set. An independent set is called a maximal independent set when it is not a subset of any other independent set. In other words, there is no node outside the set that can be added to the set with the set remaining independent.

Below you can see the two maximal independent sets of a star graph:

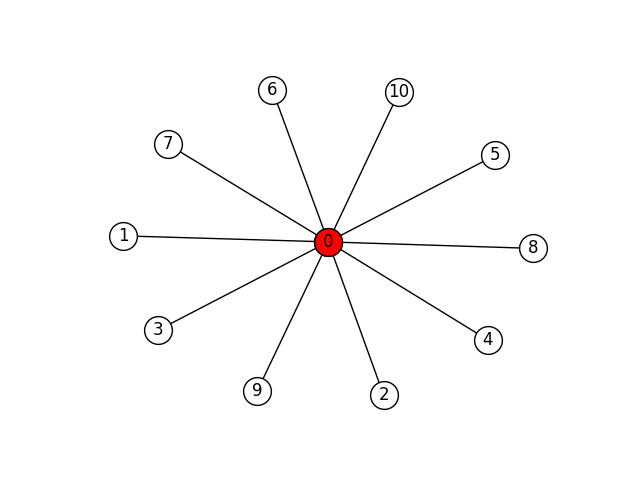
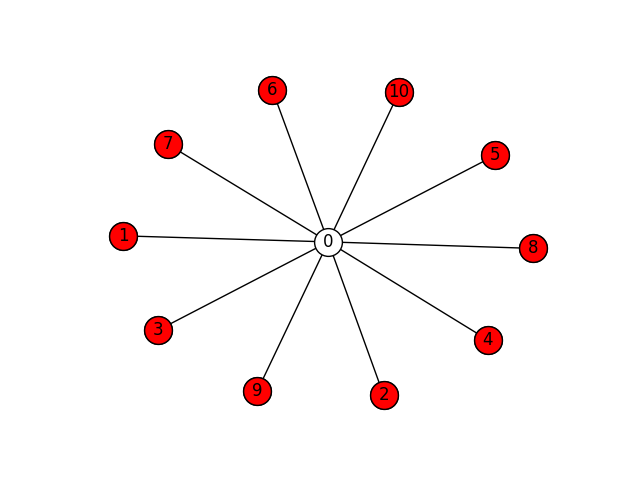
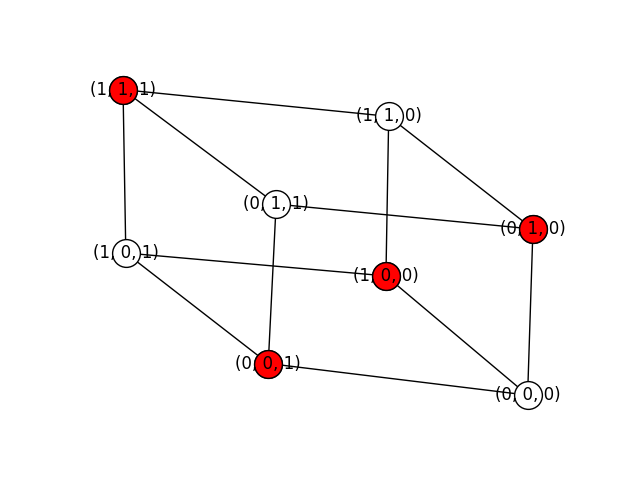
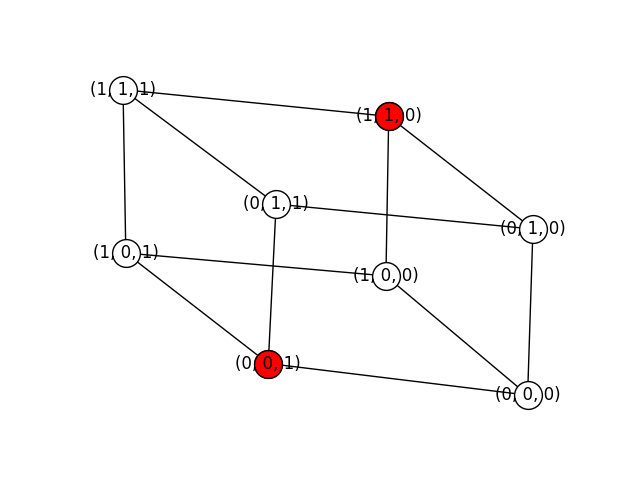
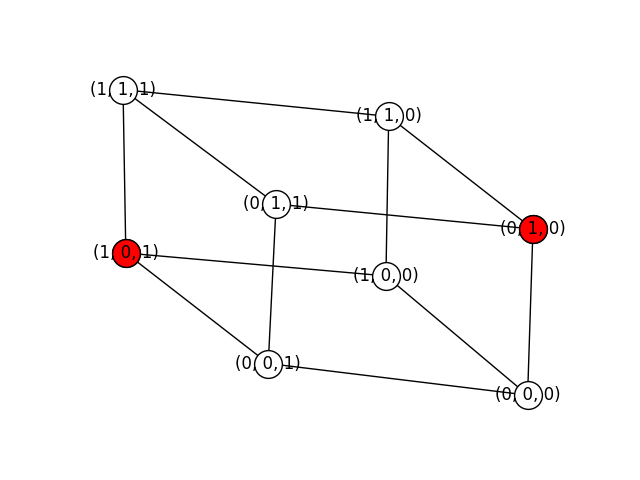
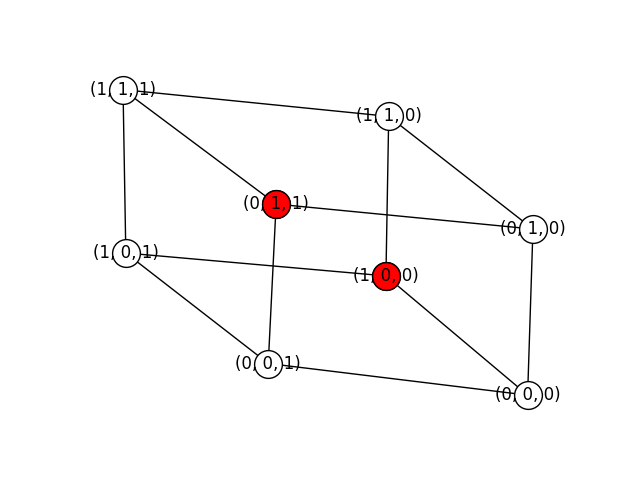
Similarly, below you can see the six maximal independent sets of a cube graph:

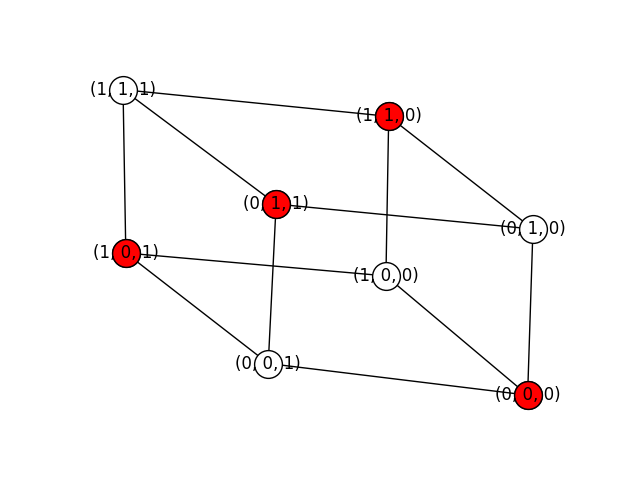
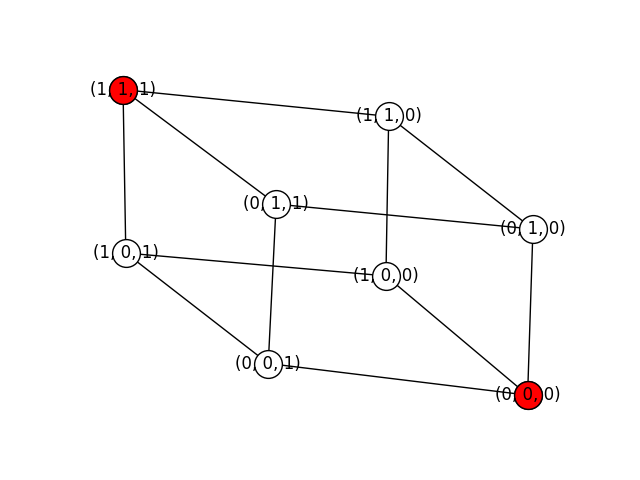
Finally, here are four maximal independent sets of the Petersen graph (there are more):

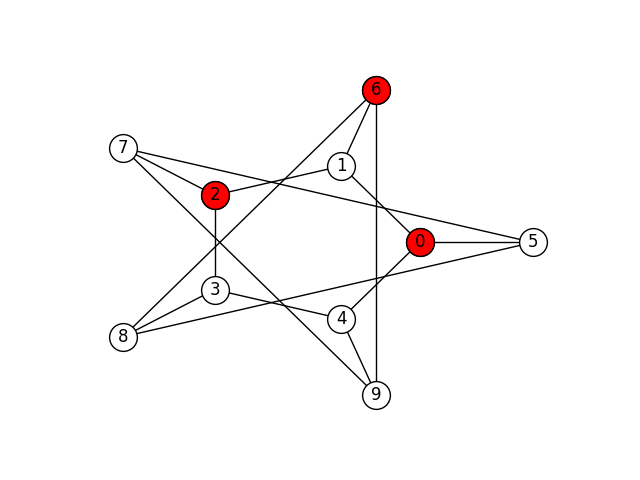
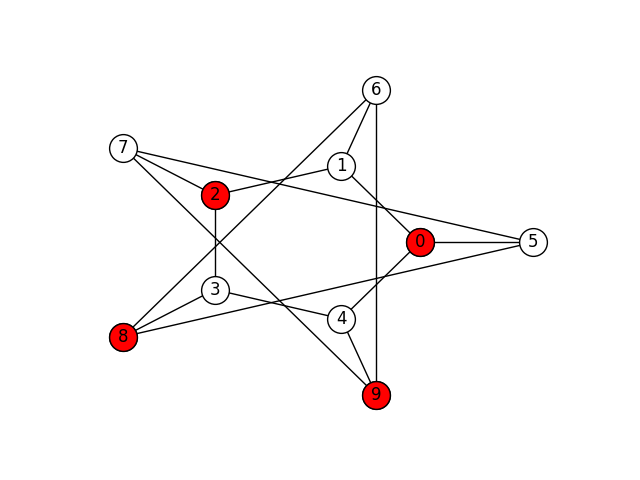
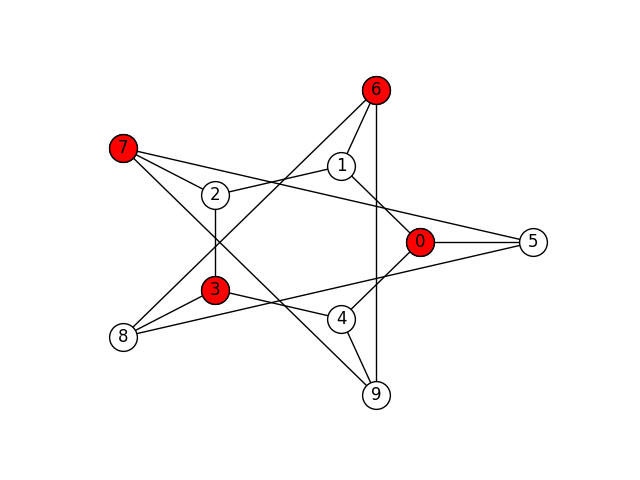
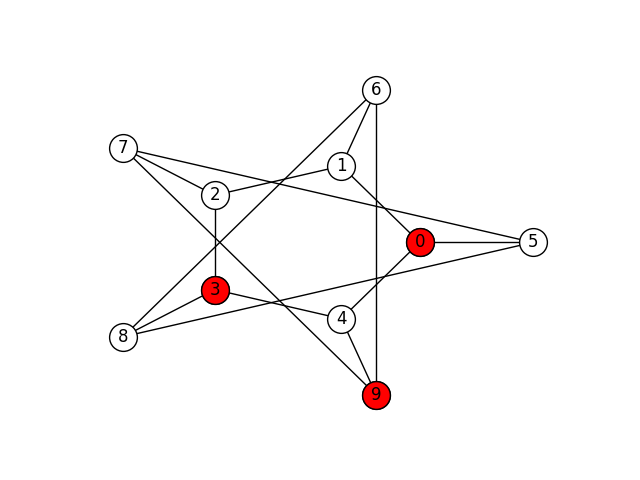
In this assignment you will implement a program that finds the maximal independent subsets of a graph.

Requirements

1. You will write a program called mis.py that finds the maximal independent subsets of a graph using the algorithm of Johnson, Yannakakis and Papadimitriou, described in [1].
2. You can use the networkx library for graph input, output, manipulation, and drawing.
3. You can use anything you want from the Python library.
4. The program must be called as follows:

python mis.py [-h] [-d] [-n NAME] [-f FIGURE] input

The input parameter corresponds to the name of the file containing the graph. The file will contain the graph in networkx adjacency list format.

If the user provides the parameter -d, the program will display on screen the graph and each maximal independent subset, similarly to the way we have presented them here. The actual images produced need not be exactly the same as the one we have shown, as graph layout depends on many parameters.

If the user provides the parameter -n NAME and -f FIGURE each images will be stored in a file with name NAME_x.FIGURE, where x is a positive number. For example, if the user enters -n cube -f png, the program will store the images in the files cube_1.png, cube_2.png, and so on.

The parameter -h can be used to display a short description of the program and its parameters.

In all cases, the program output will be the maximal independend subsets in lexicographic order. So, if we are dealing with the star graph, the output will be:

['0']
['1', '10', '2', '3', '4', '5', '6', '7', '8', '9']

While if we are dealing with the cube graph, the output will be:

['(0, 0, 0)', '(0, 1, 1)', '(1, 0, 1)', '(1, 1, 0)']
['(0, 0, 0)', '(1, 1, 1)']
['(0, 0, 1)', '(0, 1, 0)', '(1, 0, 0)', '(1, 1, 1)']
['(0, 0, 1)', '(1, 1, 0)']
['(0, 1, 0)', '(1, 0, 1)']
['(0, 1, 1)', '(1, 0, 0)']

Graph Examples

You can check your program with the following files:

• Star graph with 10 nodes.
• Cube graph.
• Petersen graph.
• Barabási-Albert graph with 15 nodes.
• Powerlaw cluster graph with 20 nodes.
• Erdős-Rényi graph with 20 nodes.
• Erdős-Rényi graph with 25 nodes.

Bibliography