Real World Algorithms

Imagine that you have a set of points on a plane and you want to cover them with a set of straight lines. Can you find the mininum number of straight lines passing through the points so that you cover all of them?

This is the so-called hitting objects, or point cover, or line cover, or point line cover problem. The first name comes from the analogy of a set of objects that we want to hit with the minimum number of shots. Of course, the problem is more general than just an application of ballistics or optimizing a bombing campaign. You may need to find the minimum number of straight segments that lie on a number of facilities on the plain, such as irrigation channels connecting reservoirs. Be it as it may, this assignment is titled "Covering Points", instead of "Hitting Objects", to defuse any trigger-happy connotation.

For example, see the following figure, which shows 18 points.

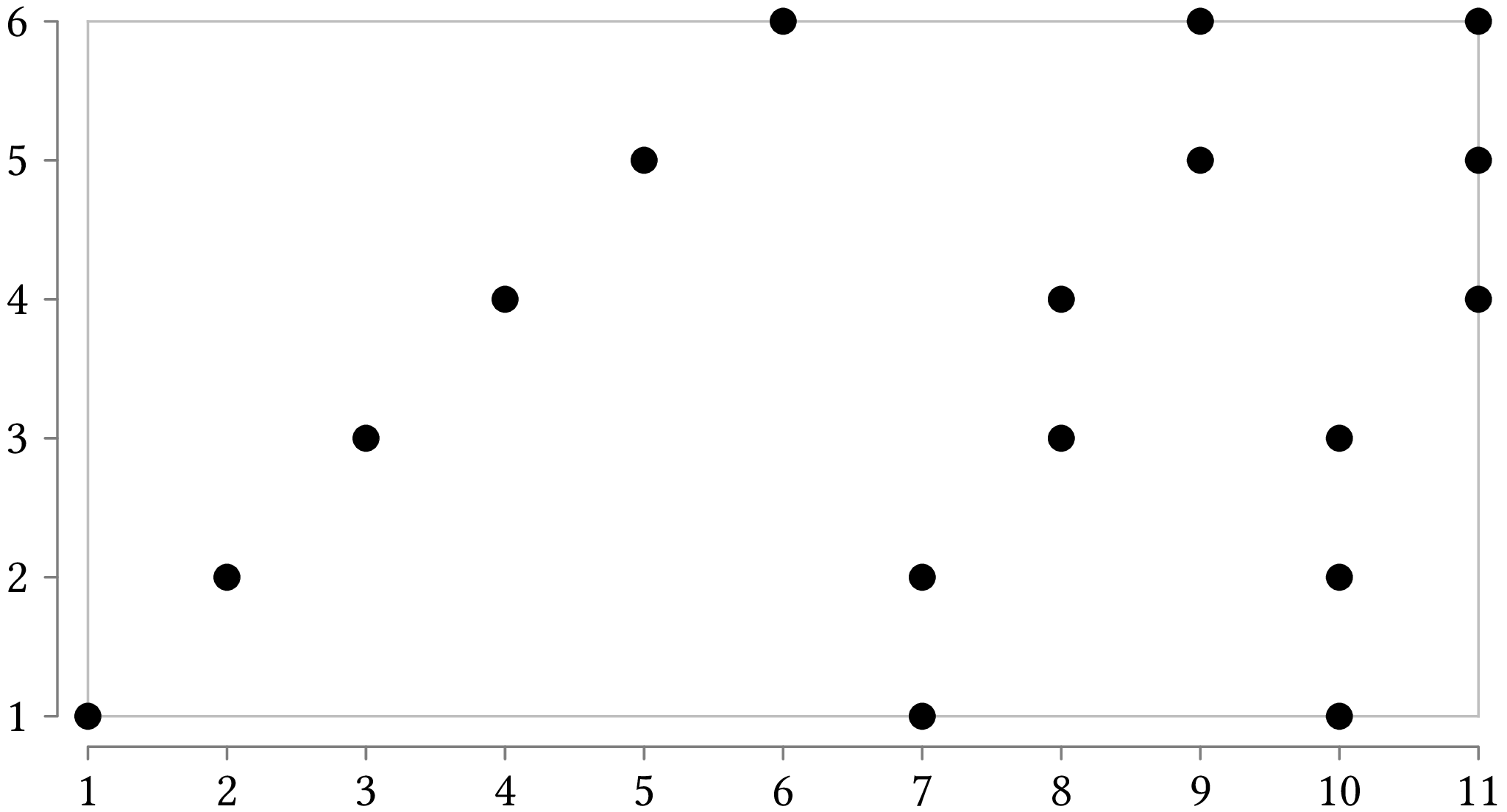
We can cover these points using five lines, like this:

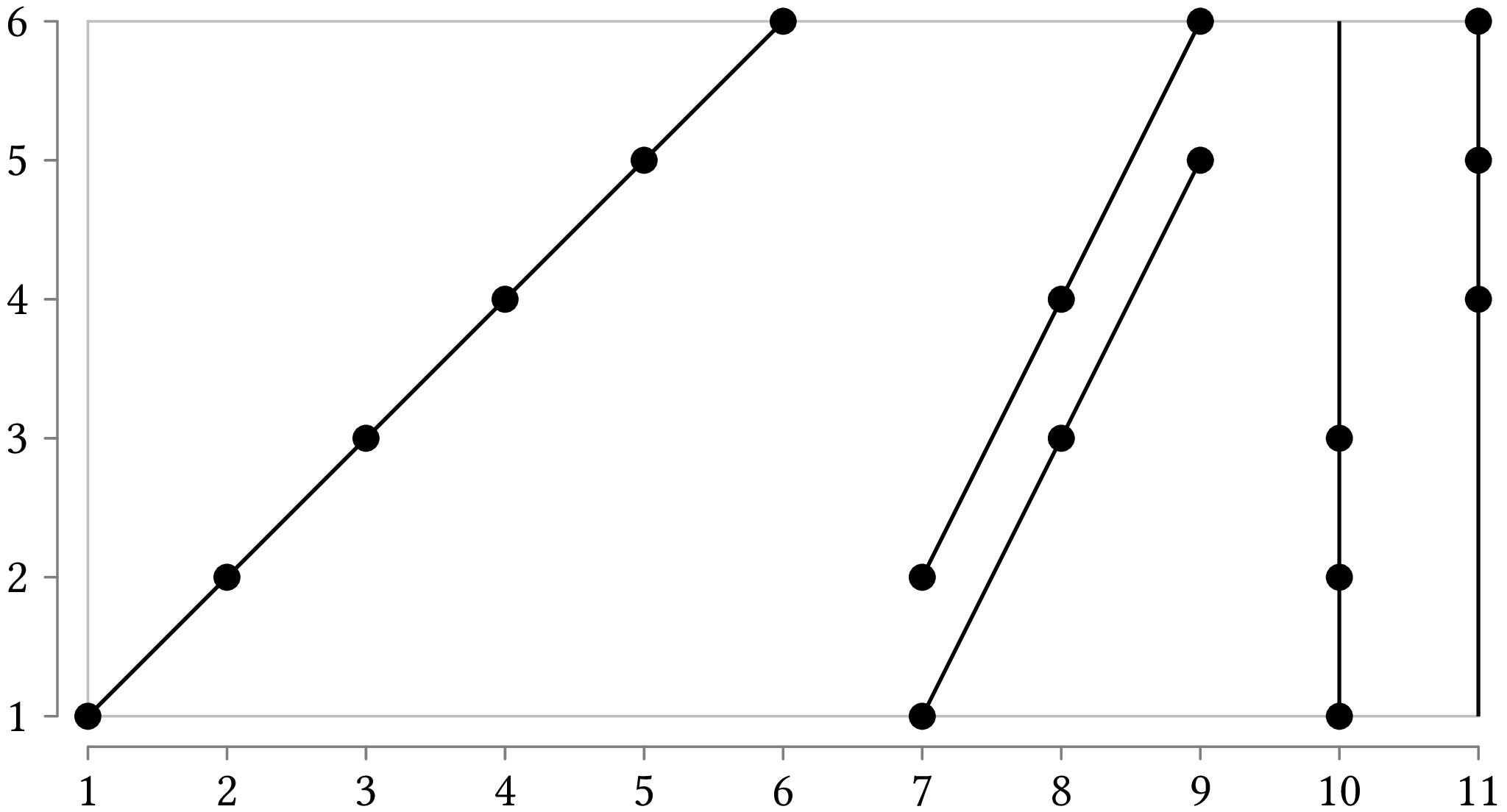
Alternatively, if we have the additional requirement that the lines should be horizontal or vertical, then the optimum solution uses six lines:

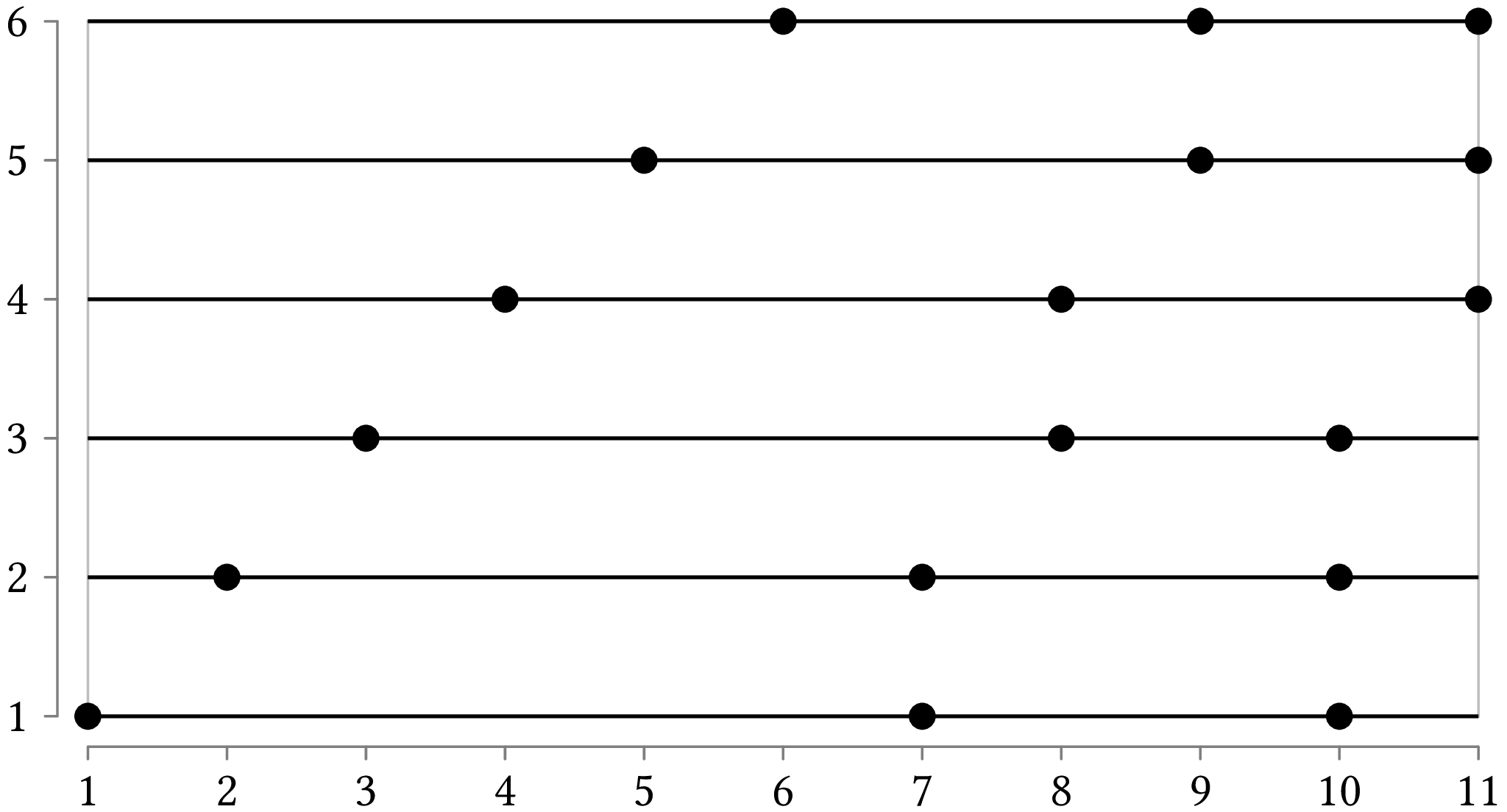
The question is, how do we go about finding these solutions?

Solution Method

Selecting the minimum number of lines passing through a set of points is a geometric version of the more general set covering problem. This is defined as follows: If we have a set of elements, which we call universe, $U = {1, 2, \ldots n}$, and a set $S$ of $m$ sets whose union equals the universe, find the smallest subset of $S$ whose union equals the universe. The set covering problem is equivalent to the points covering problem if we take $U$ to be the set of points that we want to cover and $S$ the set of lines passing through the points (each line defined by the points it goes through).

For example, let's have as universe $U = {1, 2, 3, 4, 5}$ and the set of sets $S = {{1}, {1, 2}, {1, 2, 3}, {2, 4}, {3, 4}, {4, 5}}$. We can see that the union of all members of $S$ gives us $U$, but we can also cover $U$ using the ${{1, 2, 3}, {4, 5}}$ subset of $S$.

Unfortunately, the set covering problem cannot be solved in polynomial time. Indeed, take this approach:

• For every possible subset of $S$:
  • Check if it covers $U$.
  • If yes, and it is smaller than the best candidate solution that we have found so far, note it as the best candidate solution.

When these steps finish, the final candidate solution will also be the best. The problem lies in the phrase "for every possible subset of $S$". If a set contains $m$ elements, the number of possible subsets is $2^m$; therefore, unless $m$ is small, there is no way we can find the solution in a reasonable amount of time.

Of course, if you think about it, you do not need to check every possible subset of $S$. As we want the minimum number of elements, or to be more specific, lines, we can improve our approach:

• Enumerate the subsets of $S$ in increasing size (number of lines):

• Check if the current subset covers $U$.

• If yes, that is the solution we are looking for and we can stop.

This will give us the best solution. If we go on without stopping, we may find another solution with the same number of lines, which won't improve on what we have already found, or with a larger number of lines, which we don't want.

The problem remains that even this improved approach will not necessarily run in a reasonable amount of time. The points that we want to cover may be placed in way that only pairs of them are colinear. Then, if we have $n$ points, we need $n/2$ lines to cover them, but we don't know that beforehand. We will start checking with the smallest number of lines and then go on increasing the number of lines until we get to the required $n/2$ lines:

• Subsets with zero lines (the empty subset).

• Subsets containing only one line (these will cover only two points each).

• Subsets containing two lines (these will cover only four points each).

• And so and so forth, until we arrive at a subset containing $n/2$ lines.

So, in the end, we will still need to check an exponential number of subsets, of the order of $2^{n/2}$. Now, you may observe that we don't need to check subsets with zero lines or one line, but that is just a drop in the ocean of possible solutions that we have to check. If you want to see an example of points that are only pairwise colinear, check the No-three-in-line problem.

Alternatively, we can use a different approach, which will complete fast, but it is not guaranteed to come up with the best solution:

• Start with a new, empty solution.

• While not all elements of $U$ have been covered:

  • Find the member of $S$ that covers the greatest number of uncovered elements and add them to the solution.

This approach is a greedy algorithm, because at each step in the iteration it proceeds by opting for the maximum immediate payoff (the maximum number of elements that can be covered at that point). But this does not ensure that at the end we will have the best solution overall. As we know, delayed gratification has something going for it, and a greedy algorithm may have to pay a price in the long run. If we return to the example with the points and the lines that run horizontally or vertically, a greedy algorithm could finish with the following solution, instead of the best one:

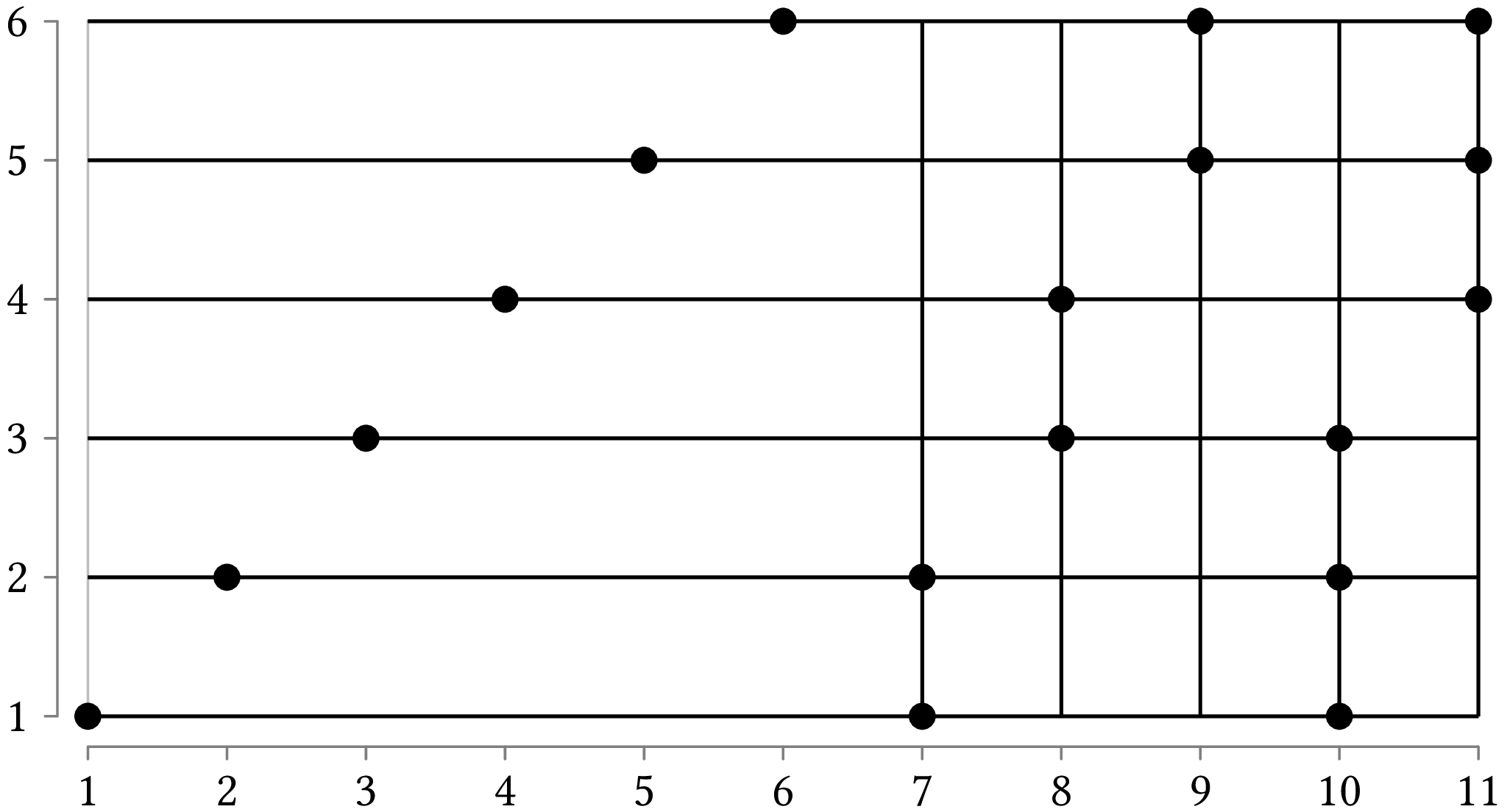
How can this happen? The greedy algorithm may select the vertical line that cuts the horizontal axis at 11, then the vertical line that cuts the horizontal axis at 10, and so on, adding vertical lines to the solution until it reaches 7 on the horizontal axis. Then it will have to cover the remaining points with abscissae 1 to 6 by adding horizontal lines to the solution.

Requirements

You will write a program called points_cover.py. You may use the following libraries: itertools, argparse or sys (in particular, the list sys.argv) to handle program arguments.

Your program will be called as follows:

python points_cover.py [-f] [-g] points_file

The meaning of the program arguments is:

• The argument-f (full exploration), if given, instructs the program to find the best solution, examining as many subsets as needed. If the problem is small, that is, there are few lines, the program should finish relatively fast. If the problem is not small then the program may take, literally, ages to finish, but that is not your problem. If the argument -f is not given, the program will execute the greedy algorithm.

• The argument -g (grid), if given, instructs the program to find only lines that are horizontal or vertical. If it is not given, the program may use any lines that pass through the points.

• The argument points_file is the name of the file that contains the points we want to cover. The file consists of lines of the form:
  text x y
  where x is the $x$-axis coordinate and y is the $y$-axis coordinate of each point.

If we specify -g and it is not possible to cover all points with lines passing through at least two of them, you may use horizontal lines that pass through the points that are not colinear with another point in the horizontal or vertical direction. So, if there is a point $(x, y)$ and there is no point $(x', y)$ or $(x, y')$, you can use the line passing through $((x, y), (x + 1, y))$.

The lines that will make up your solutions must appear in descending order based on the number of points they cover. In other words, lines covering more points will precede lines covering fewer points. For each line, the point it covers will appear in ascending order, based on their coordinates. Lines covering the same number of points will appear in ascending order, depending on the coordinates of their points.

Depending on your implementation, you may need to sort the input points you read from points_file.

Examples

Example 1

If you invoke the program with:

python points_cover.py example_1.txt

then the program will read the file example_1.txt and will display the following results:

(1, 1) (2, 2) (3, 3) (4, 4) (5, 5) (6, 6)
(7, 1) (8, 3) (9, 5)
(7, 2) (8, 4) (9, 6)
(10, 1) (10, 2) (10, 3)
(11, 4) (11, 5) (11, 6)

This is the first solution we saw for covering the 18 points given in the beginning of this assignment.

Example 2

If you invoke the program with:

python points_cover.py -f -g example_1.txt

then the program will read the file example_1.txt and will display the following results:

(1, 1) (7, 1) (10, 1)
(2, 2) (7, 2) (10, 2)
(3, 3) (8, 3) (10, 3)
(4, 4) (8, 4) (11, 4)
(5, 5) (9, 5) (11, 5)
(6, 6) (9, 6) (11, 6)

This is the second solution we saw for covering the 18 points given in the beginning of this assignment.

Example 3

If you invoke the program with:

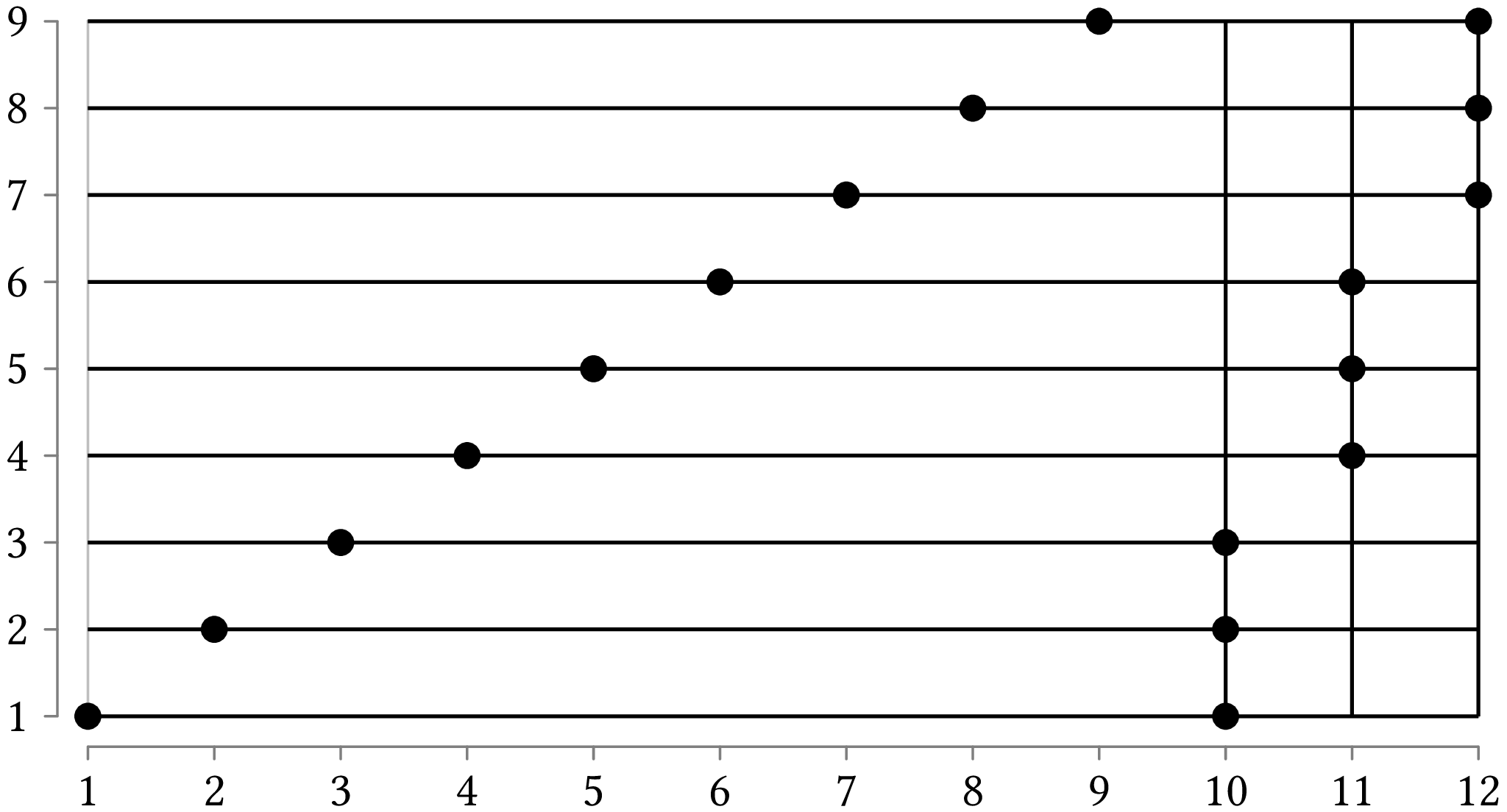
python points_cover.py -g example_2.txt

then the program will read the file example_2.txt and will display the following results:

(10, 1) (10, 2) (10, 3)
(11, 4) (11, 5) (11, 6)
(12, 7) (12, 8) (12, 9)
(1, 1) (10, 1)
(2, 2) (10, 2)
(3, 3) (10, 3)
(4, 4) (11, 4)
(5, 5) (11, 5)
(6, 6) (11, 6)
(7, 7) (12, 7)
(8, 8) (12, 8)
(9, 9) (12, 9)

Example 4

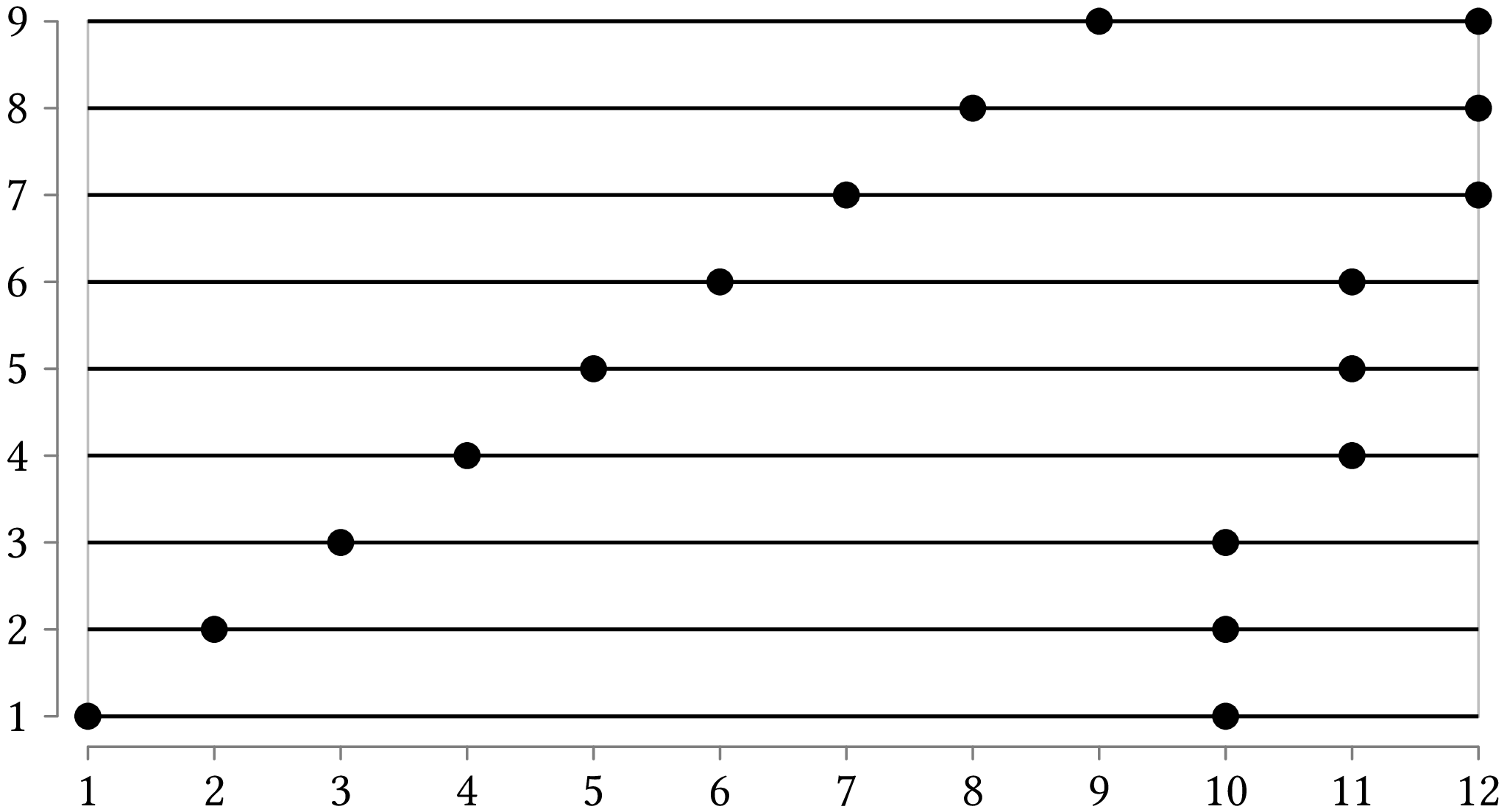
If you invoke the program with:

python points_cover.py -f -g example_2.txt

then the program will read the file example_2.txt and will display the following results:

(1, 1) (10, 1)
(2, 2) (10, 2)
(3, 3) (10, 3)
(4, 4) (11, 4)
(5, 5) (11, 5)
(6, 6) (11, 6)
(7, 7) (12, 7)
(8, 8) (12, 8)
(9, 9) (12, 9)

Example 5

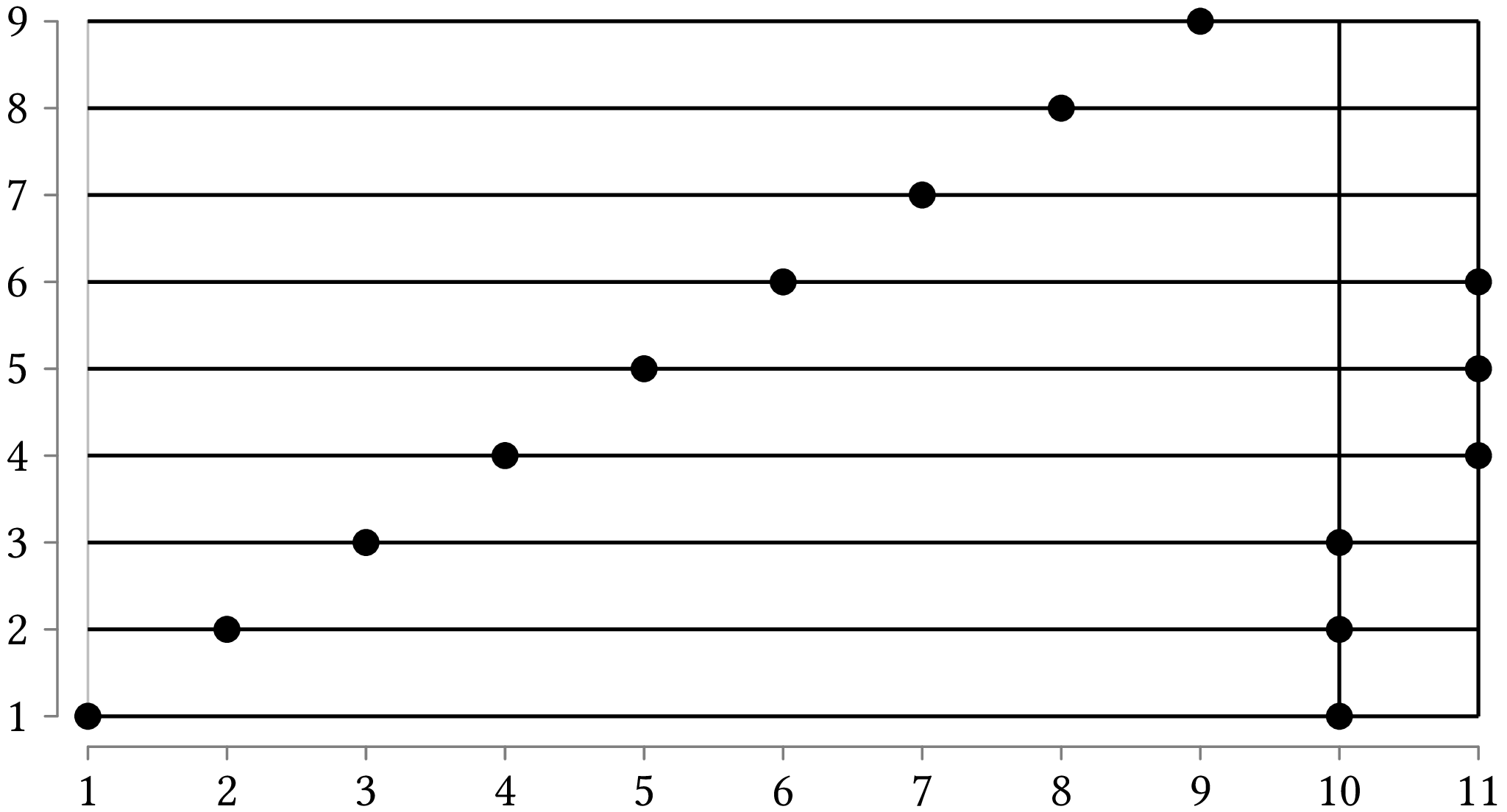
If you invoke the program with:

python points_cover.py -g example_3.txt

then the program will read the file example_3.txt and will display the following results:

(10, 1) (10, 2) (10, 3)
(11, 4) (11, 5) (11, 6)
(1, 1) (10, 1)
(2, 2) (10, 2)
(3, 3) (10, 3)
(4, 4) (11, 4)
(5, 5) (11, 5)
(6, 6) (11, 6)
(7, 7) (8, 7)
(8, 8) (9, 8)
(9, 9) (10, 9)

Example 6

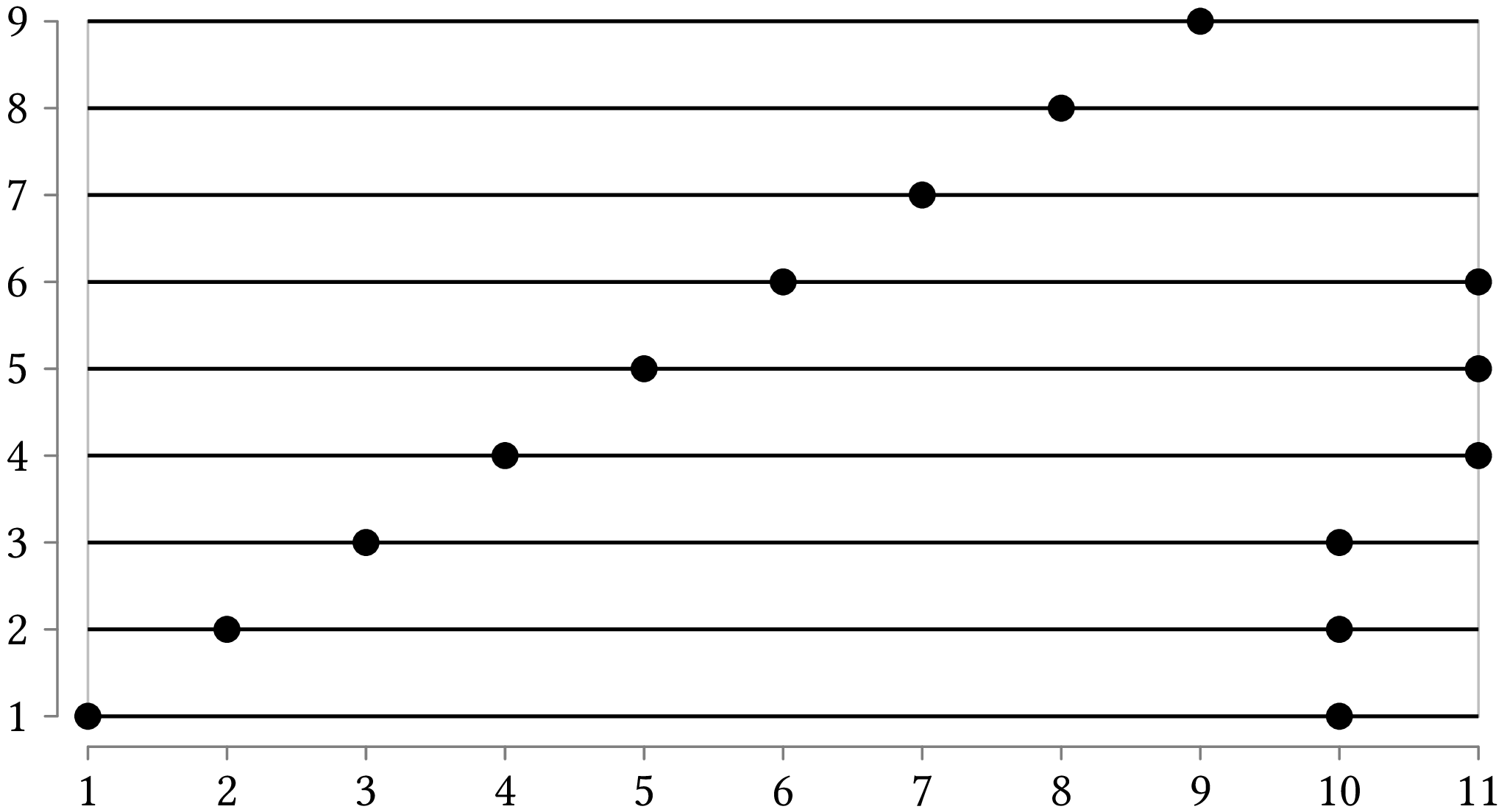
If you invoke the program with:

python points_cover.py -f -g example_3.txt

then the program will read the file example_3.txt and will display the following results:

(1, 1) (10, 1)
(2, 2) (10, 2)
(3, 3) (10, 3)
(4, 4) (11, 4)
(5, 5) (11, 5)
(6, 6) (11, 6)
(7, 7) (8, 7)
(8, 8) (9, 8)
(9, 9) (10, 9)

Notes

For the formulation of the problem as one of locating linear facilities on the plane see [4]; for its hitting objects incarnation, see [1]. A more generic treatment is to view it as covering things with things [3]. To be precise, according to [4] the point covering problem is the one we treated here; the line covering problem consists of starting with a set of straight lines and finind a minimum set of points such as each line contains at least one of them. The two problems are closely related and line covering can be reduced, i.e., recast, as point covering. For some more recent results, see [2].

Bibliography