The amount of data produced in the world is increasing rapidly, and so does the storage needed to accommodate all that data. Data centers can be bigger than football fields and require electrical power enough to power a whole city.
Scientists are trying to find more and more efficient storage media; one approach of particular interest is to use DNA for storage. With the right encoding, one cubic centimeter of DNA can store $10^{16}$ bits of data, which means that we could store all the data in the world in a kilo of DNA.
But which is the right encoding? One way to go is the following. Suppose we want to encode a file in DNA:
- We take the file contents and we encode them using base three Huffman coding. In normal Huffman coding, we encode our data using bits, that is, 0 and 1. In base three Huffman coding we encode our data using trits, that is, 0, 1, and 2.
- Base three Huffman coding works exactly like base two Huffman coding, but when we work with the priority queue, instead of taking out two elements and inserting one, we take out three elements and insert one.
- In this way we create a tree, which is triadic. Its branches correspond to 0, 1, and 2, instead of only 0 and 1. The Huffman coding results again from the paths from the root to the leaves of the tree.
- We must be careful if our file does not have an odd number of characters. As each time we modify the priority queue we take out three items and we insert one, its size is reduced by two. Therefore, if the file does not have an odd number of characters, we must add a virtual character that occurs zero times.
After encoding our file in base three Huffman code, we go on to encode the four DNA bases, A (adenine), C (cytocine), G (guanine), T (thymine). To do that, we read the encoded file trit by trit and produce DNA bases according to the following table:
| previous base | current trit | ||
|---|---|---|---|
| 0 | 1 | 2 | |
| A | C | G | T |
| C | G | T | A |
| G | T | A | C |
| T | A | C | G |
To use this table we work as follows. If we want to encode trit 2 and the previous trip that we encoded in DNA was encoded using base G, then the 2 will be encoded with base C; and so on. For the first trit, for which we have no previous one, we assume that we there was a previous virtual trit that was encoded with base A.
For example, if we want to encode a file that contains the phrase "hello, world" with a base three Huffman encoding, we will get the following tree:
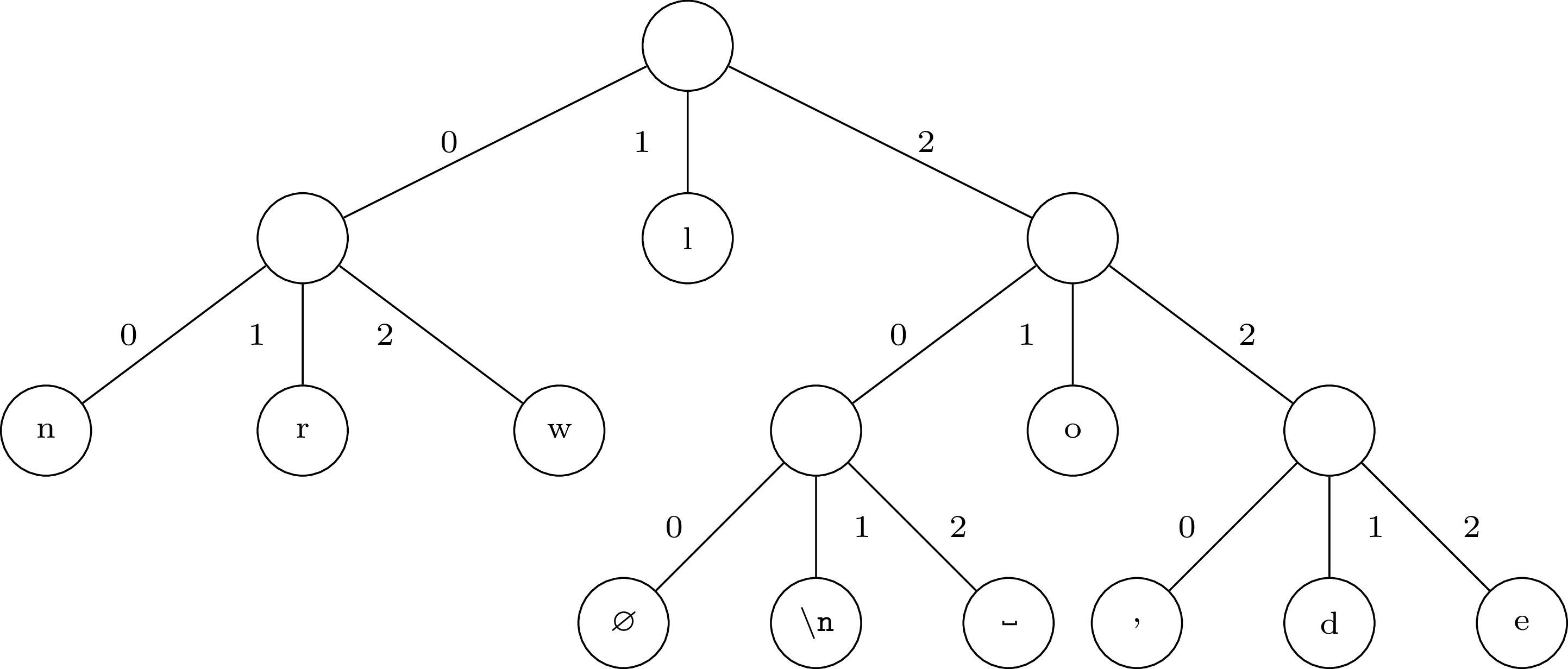
Note that the file ends in a newline character (\n), which is also
encoded. Moreover, the file has an odd number of characters, so we
have added a virtual character, which we denote by Ø. In
practice this can be simply the empty character, '', which is really
nothing—but of course it should not be the space character '
'; we use the symbol ␣ for that. The tree is essentially the
following correspondence table:
| Letter | Encoding |
|---|---|
| l | 1 |
| h | 00 |
| r | 01 |
| w | 02 |
| o | 21 |
| Ø | 200 |
| \n | 201 |
| ␣ | 202 |
| , | 220 |
| d | 221 |
| e | 222 |
With this encoding, the file with "hello, world" in it is represented as:
0022211212202020221011221201
Now, working with the table of mappings between trits and DNA bases,
the 0 will become C, the second 0 will become G, the 2 will
become C, and so on. At the end we will end up with the DNA
sequence:
CGCATCTGATGTGTGTGCTAGATGATAG
To decode this DNA sequence, we work in exactly the opposite way. We take the bases one by one and we convert them to trits using the following table:
| previous base | current base | |||
|---|---|---|---|---|
| A | C | G | T | |
| A | 0 | 1 | 2 | |
| C | 2 | 0 | 1 | |
| G | 1 | 2 | 0 | |
| T | 0 | 1 | 2 | |
The table is used as the one during encoding. In the beginning we
assume that the previous base is A. In our example, we then take
base C, which is encoded to 0. Following that, we take base G;
this time the previous page is C, so G is encoded using 0; and
so on.
After getting the corresponding trits, we convert them to the original
file contents using the base three Huffman code that we have
created. That means that 00 is converted back to h, 222 is
converted back to e, etc.
The purpose of this assignment is to implement a DNA encoding and decoding scheme; for more details on the underlying research, see [1] and [2].
Requirements
- You will write a program called
dna_store.pyto implement the DNA storage scheme we described. - You will implement your own prioriry queue for use in the program.
- Your program must be called as follows:
python dna_store.py [-d] input output huffman
If the user does not give the parameter -d, the program will read
the file given in the input parameter (that does not mean that the
file is actually called input, that is just a stand-in), it will
store the DNA encoding in the file given by the output parameter,
and will save the Huffman code in the file given by the huffman
parameter. The Huffman encoding will be stored in a
Comma Separated Values (CSV)
file. To work with such files you should use the
Python csv library.
If the user gives the parameter -d, the program will read the file
given by the input parameter, will decode it using the Huffman code
given by the huffman parameter, and will store the decoded result to
the file given by the output parameter. Remember that a file can
only be decoded correctly with the Huffman code that was used for
its encoding.
Examples
If the user gives:
python dna_store.py hello_world.txt hello_world_dna.txt hello_world_huffman.csv
using the file hello_world.txt, then the Huffman code will be stored in the file hello_world_huffman.csv and the encoded file will be hello_world_dna.txt.
If the user gives:
python dna_store.py 1984.txt 1984_dna.txt 1984_huffman.csv
with the file 1984.txt, then the Huffman code will be stored in the file 1984_huffman.csv and the encoded file will be 1984_dna.txt.
If the user gives:
python dna_store.py -d 1984_dna.txt 1984_decoded.txt 1984_huffman.csv
the file 1984_decoded.txt must be exactly the same as the file
1984.txt.
Notes on Implementation
Depending on how you implement the priority queue and the Huffman encoding, the results may differ from the ones shown above. That is fine. In any case, you can check that your program is correct by verifying that the decoding of an encoded file is the original file.
Bibliography
- Andy Extance. How DNA could store all the world's data. Nature, 537(7618):22–14, August 31 2016. ↩
- Nick Goldman, Paul Bertone, Chen, Siyuan, Dessimoz, Christophe, LeProust, Emily M., Sipos, Botond, and Ewan Birney. Towards practical, high-capacity, low-maintenance information storage in synthesized DNA. Nature, 494(7435):77–80, February 3 2013. ↩
