Real World Algorithms

One of the most important scientific developments of the last decades has been the decoding of the human genome. Thanks to the techniques that were developed in that effort, we can now investigate genetic diseases, detect mutations, study genomes of extinct species, among other fascinating applications.

Genomes are encoded in the DNA, a large organic molecule that is composed of a double helix. The double helix is made up of four bases: cytosine (C), guanine (G), adenine (A), and thymine (T). Each part of the double helix is constructed from a series of bases, like ACCGTATAG. The other part of the double helix is constructed from bases that are connected with their corresponding bases on the first part, according to the rules A-T, C-G. So, if one part of the helix is ACCGTATAG, the other part will be TGGCATATC.

In order to find the composition of an unknown DNA piece, we work as follows. We create many copies of the chain and we break them up into little fragments, for instance, fragments containing three bases each. Using specialized instruments we can identify such small fragments easily. In this way we end up with a set of known fragments. We are then left with the problem of assembling the fragments to a DNA sequence, whose composition we will then know.

Suppose then that we have the following fragments, or polymers as they are known: GTG, TGG, ATG, GGC, GCG, CGT, GCA, TGC, CAA, AAT. Each one of them has length 3, but in general they can have length $k$. To find the DNA sequence from which they were broken up, we create a graph. In that graph, the vertices are polymers of length 2 (or, more generally, $k - 1$) that are derived from the polymers of length 3 (or, $k$ in the general case), taking for each polymer of length 3 ($k$) the first 2 ($k - 1$) and the last 2 ($k - 1$) polymers. So, from GTG we will get GT and TG, from TGG we will get TG and GG. In the graph we add one edge for every one of the initial polymers or length 3 ($k$) that was used to derive the two vertices. We give the name of the polymer to that edge. So, from ATG we got vertices AT and TG and the edge ATG. You can see the graph that results from our example:

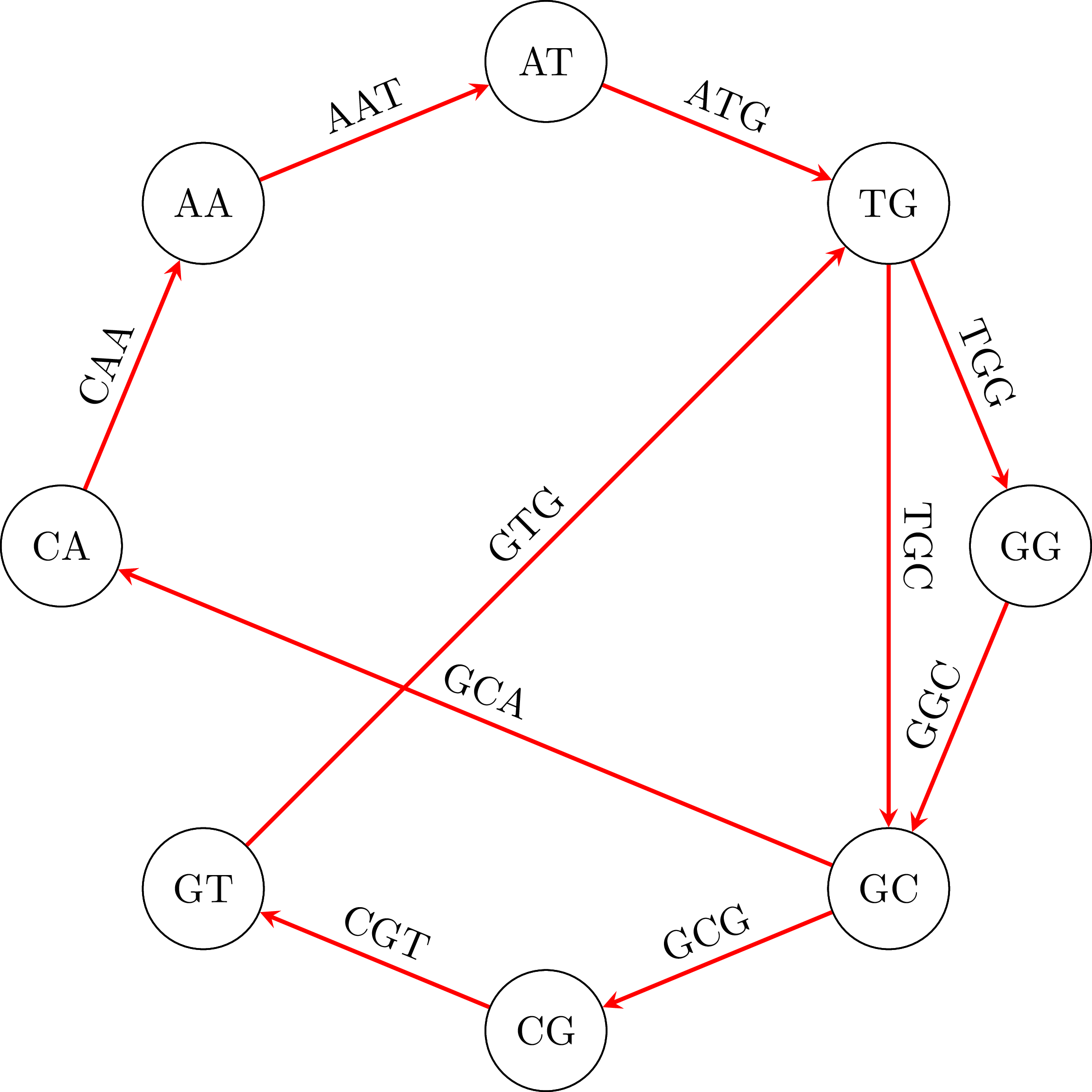
To find the initial DNA sequence we only need to find a path in the graph that visits all edges exactly once. We call a path with this property Eulerian path and it exists if and only if each vertex has the same in-degree and out-degree and all vertices with non-zero degree belong to a single strongly connected component.

To find the path that we want in the graph that we created, we use Hierholzer's algorithm:

• We pick a starting node, $u$.
• We go from node to node until we return to $u$. The path that we have traced to this point does not necessarily cover all edges.
• As long as there exists a vertex $v$ that belongs to the path we have traced, but is part of an edge that does not belong to that path:
  • We start another path from $v$, using edges that we have not used yet, until we return to $v$. Then we splice this path to the path we have already traced.

If we use the algorithm in our example graph, we will find the path in the following figure:

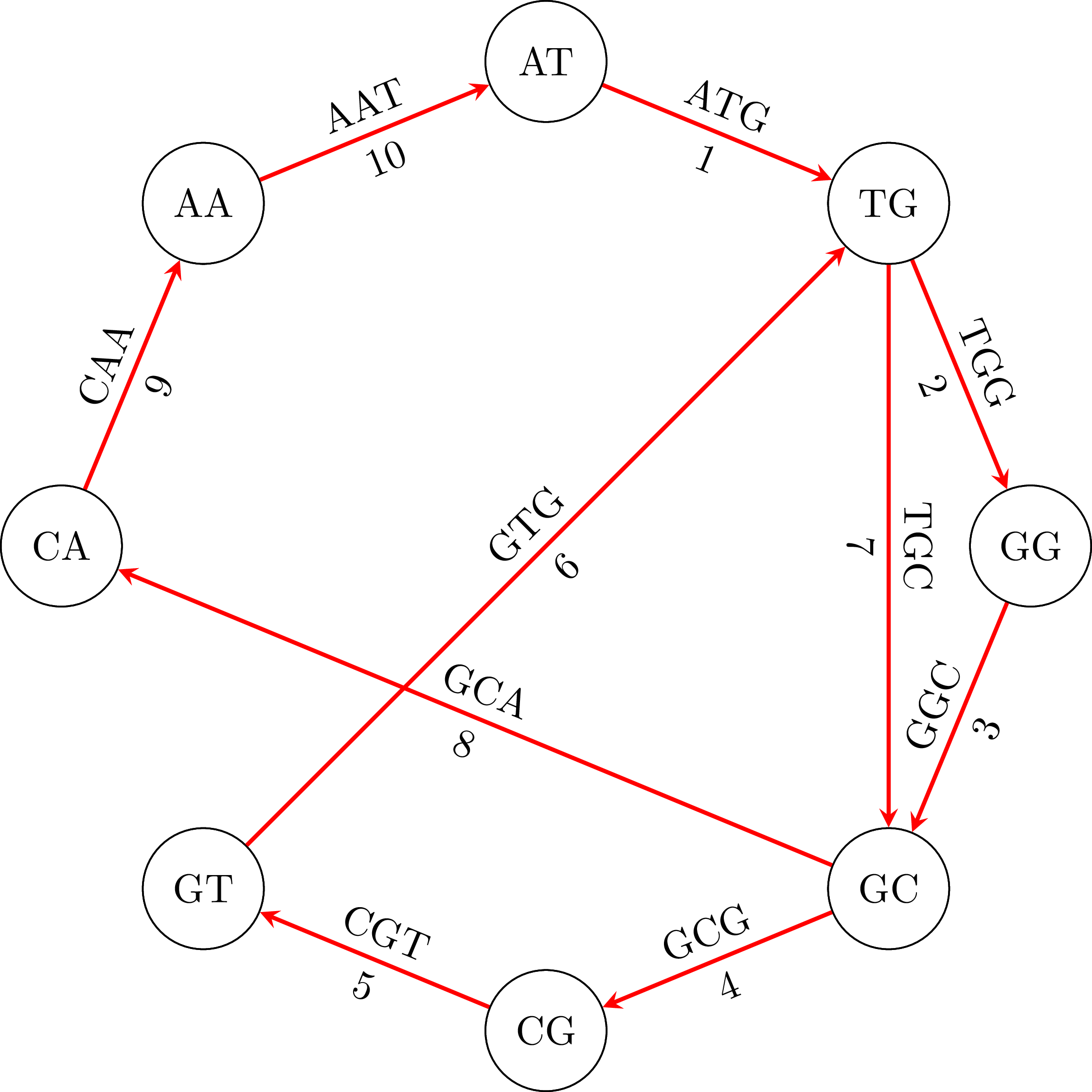
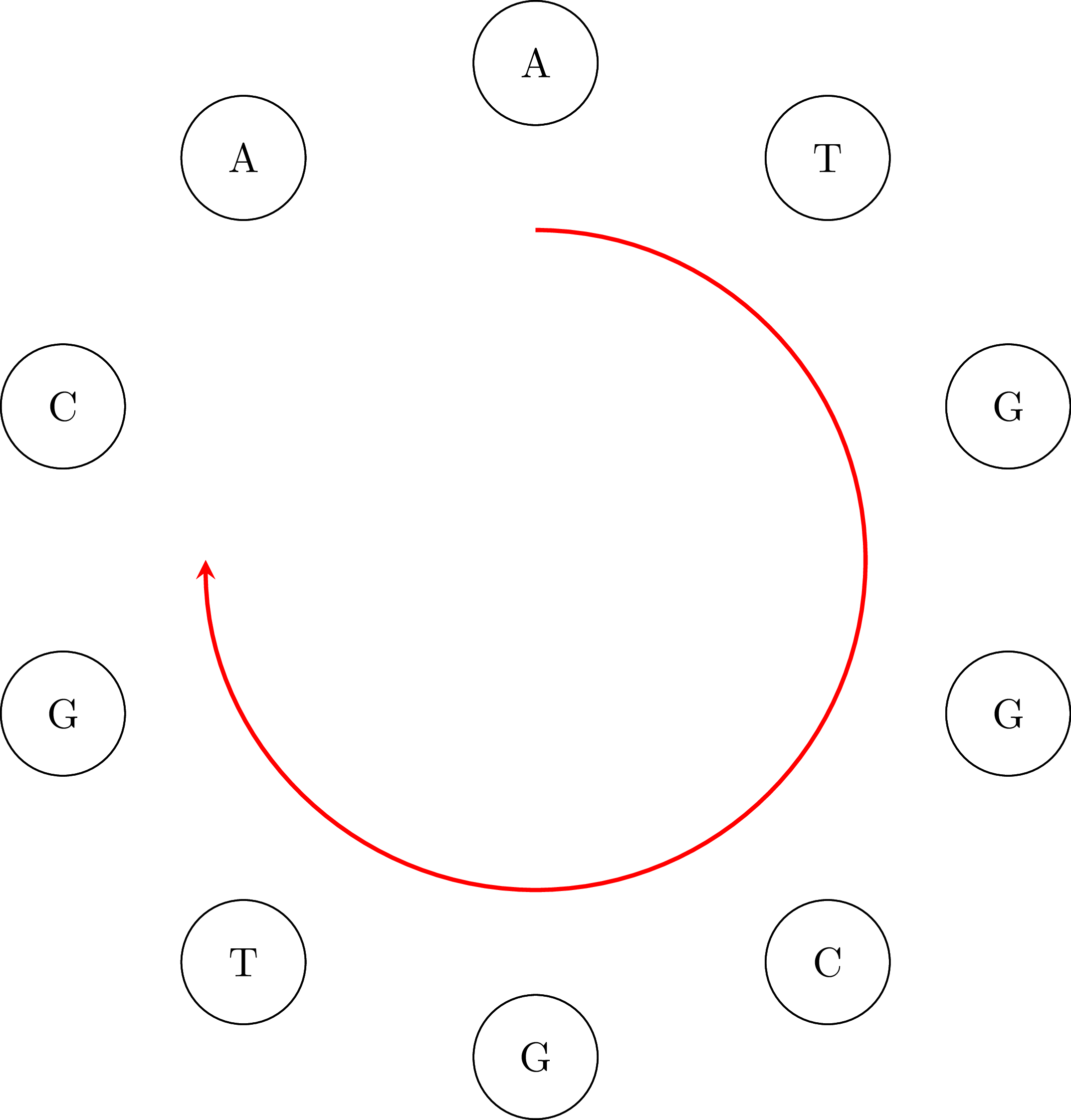
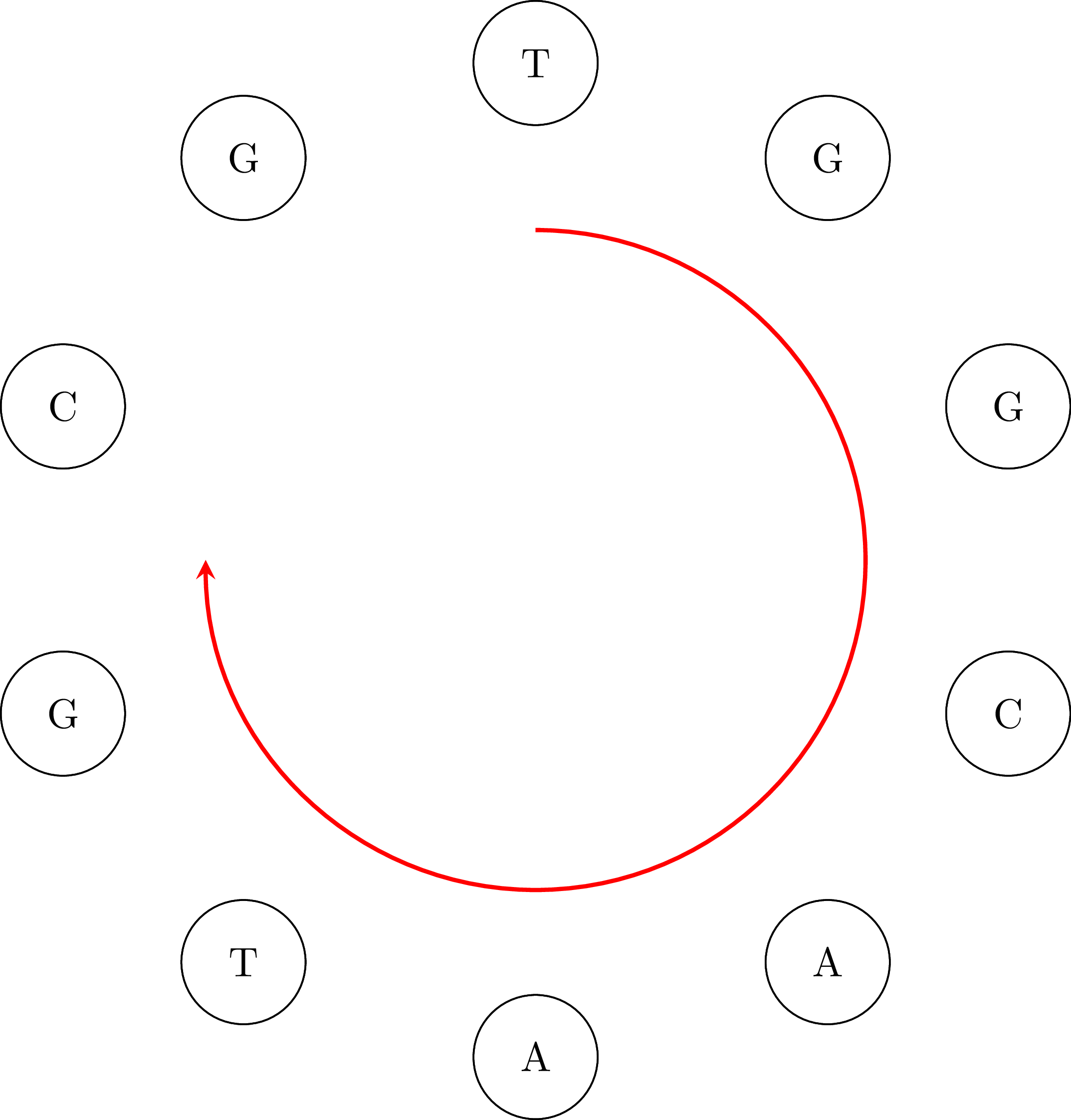
If we go along the path and we connect the vertices keeping their common base only once we get the DNA sequence ATGGCGTGCA. Note that the sequence is cyclical: the vertex AA occurs in the sequence if we connect its end with its beginning. That means that an equivalent sequence is GGCGTGCAAT, or any other that is a rotation of ATGGCGTGCA. Moreover, depending on the starting node $u$ and how we choose an edge when we have more than one outgoing vertices, we may get a different sequence. For example, if we start from TG we may get the sequence TGGCAATGCG or any other that is a rotation of TGGCAATGCG. That is OK. In the following figures you can see the cyclical character of the sequences:

    

The purpose of this assignment is to create a program that assembles DNA from a set of fragments. For more details, see [1] and [3]. Hierholzer's algorithm was originally published in 1873 [2].

Requirements

1. You will write a program named dna_assembly.py that performs DNA assembly.
2. You will not use ready-made graph libraries.
3. Your program must be called as follows:

python  dna_assembly.py fragments_file

The fragments_file argument specifies the name of the file where the DNA fragments are stored. The file will have the following format:

ATG
GTG
TGG
GGC
GCG
CGT
GCA
TGC
CAA
AAT
ATG
AAT
...

that is, it contains one polymer per line.

Output

The program's output will be the DNA sequence that it assembled.

Examples

The fragments for the example that we have been using is in the file fragment_file_1.txt, so the output will be:

ATGGCGTGCA

or some other equivalent sequence, as explained above.

If the user gives the file fragment_file_2.txt the output will be:

AGTGGACCATGTATACTTCA

or some other equivalent, such as:

TGTACTTCATATGGACCAAG

If the user gives the file fragment_file_3.txt the output will be:

ATCTCAGACTTACACCATATGG

or some other equivalent, such as:

TCTCAGACTTACACCATATGGA

If the user gives the file fragments_file_4.txt the output will be:

GACTACCTGGTCTCGATCACGGA

or some other equivalent, such as:

CGGTCACTCTGGACCTACGAGAT

or:

TACTCGGACGAGATCACCTGGTC

If you want to verify the results, you can write some code that checks that:

1. All the fragments in the input file are present in the output sequence.
2. All the fragments in the sequence are present in the input file.

Bibliography